题目内容
6.已知函数$f(x)=\left\{\begin{array}{l}{x^2}-2ax+5,x<1\\ 1+\frac{1}{x},x≥1\end{array}\right.$在R上单调,则实数a的取值范围是[1,2].分析 由于函数f(x在定义域R上单调,可得函数在R上单调递减,故有$\left\{\begin{array}{l}{a≥1}\\{1-2a+5≥1+1}\end{array}\right.$,即可求出实数a的取值范围.
解答 解:由于函数f(x)在定义域R上单调,可得函数在R上单调递减,
故有$\left\{\begin{array}{l}{a≥1}\\{1-2a+5≥1+1}\end{array}\right.$,解得1≤a≤2,即[1,2].
故答案为:[1,2].
点评 本题考查分段函数的单调性,考查学生分析解决问题的能力,正确转化是关键.

练习册系列答案
相关题目
16.阅读如图的算法框图,输出的结果S的值为( )
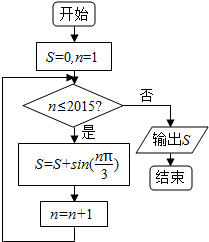

| A. | $\frac{{\sqrt{3}}}{2}$ | B. | 0 | C. | $\sqrt{3}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
18.若命题p:?x0∈R,x02+x0+1<0,则¬p为( )
| A. | ?x∈R,x2+x+1<0 | B. | ?x∈R,x2+x+1>0 | C. | ?x∈R,x2+x+1≥0 | D. | ?x∈R,x2+x+1≥0 |