题目内容
4.已知向量$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(x,-6),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=5$\sqrt{2}$.分析 由向量垂直的条件:数量积为0,可得x=3,再由向量模的公式,计算即可得到所求.
解答 解:向量$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(x,-6),
若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则$\overrightarrow{a}$•$\overrightarrow{b}$=2x-6=0,
解得x=3,
即有$\overrightarrow{a}$+$\overrightarrow{b}$=(5,-5),
则|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{{5}^{2}+(-5)^{2}}$=5$\sqrt{2}$,
故答案为:5$\sqrt{2}$.
点评 本题考查向量的垂直的条件:数量积为0,考查向量的模的计算,属于基础题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
13.等差数列{an}中,a5、a7是函数f(x)=x2-4x+3的两个零点,则a3+a9等于( )
| A. | -4 | B. | -3 | C. | 3 | D. | 4 |
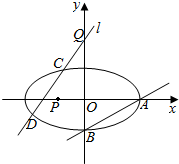 已知椭圆M:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$ (a>b>0)的离心率e=$\frac{\sqrt{6}}{3}$,过点A(a,0)和B(0,-b)的直线与原点的距离为$\frac{\sqrt{3}}{2}$.
已知椭圆M:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$ (a>b>0)的离心率e=$\frac{\sqrt{6}}{3}$,过点A(a,0)和B(0,-b)的直线与原点的距离为$\frac{\sqrt{3}}{2}$.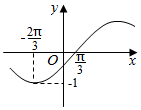 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象如图:
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象如图: