题目内容
11.从一个正方体中截去部分几何体,得到的剩余几何体的三视图如图,则此几何体的体积是( )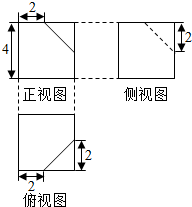
| A. | 64 | B. | $\frac{122}{3}$ | C. | $\frac{188}{3}$ | D. | $\frac{47}{6}$ |
分析 几何体为正方体切去一个小三棱锥得到的,使用作差法求出体积.
解答 解:由三视图可知几何体为正方体切去一个小三棱锥得到的,正方体的边长为4,小三棱锥的底面直角边为2,高为2,
所以几何体的体积V=43-$\frac{1}{3}×\frac{1}{2}×2×2×2$=$\frac{188}{3}$.
故选C.
点评 本题考查了空间几何体的结构特征和三视图,属于基础题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
2.如图为某几何体的三视图,则该几体的体积为( )
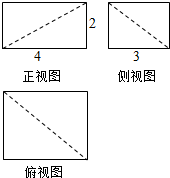

| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
6.函数f(x)=x3的图象经过( )
| A. | 第一、三象限 | B. | 第二、三象限 | C. | 第一、二象限 | D. | 第一、四象限 |
20.已知a=ln$\frac{3}{4}$,b=5lg3,c=3${\;}^{-\frac{1}{2}}$,则a,b,c的大小关系为( )
| A. | a<b<c | B. | a<c<b | C. | b<a<c | D. | b<c<a |

 在一次全国高中五省大联考中,有90万的学生参加,考后对所有学生成绩统计发现,英语成绩服从正态分布N(μ,σ2),如表用茎叶图列举了20名学生英语的成绩,巧合的是这20个数据的平均数和方差恰比所有90万个数据的平均数和方差都多0.9,且这20个数据的方差为49.9.
在一次全国高中五省大联考中,有90万的学生参加,考后对所有学生成绩统计发现,英语成绩服从正态分布N(μ,σ2),如表用茎叶图列举了20名学生英语的成绩,巧合的是这20个数据的平均数和方差恰比所有90万个数据的平均数和方差都多0.9,且这20个数据的方差为49.9.