题目内容
7.在空间四边形OABC中,G是△ABC的重心,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{OG}$=( )| A. | $\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | C. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | D. | 3$\overrightarrow{a}$+3$\overrightarrow{b}$+3$\overrightarrow{c}$ |
分析 由题意知$\overrightarrow{AG}$=$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),从而化简可得.
解答 解:∵G是△ABC的重心,
∴$\overrightarrow{AG}$=$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),
∴$\overrightarrow{OG}$=$\overrightarrow{OA}$+$\overrightarrow{AG}$
=$\overrightarrow{OA}$+$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)
=$\overrightarrow{OA}$+$\frac{1}{3}$($\overrightarrow{OB}$-$\overrightarrow{OA}$+$\overrightarrow{OC}$-$\overrightarrow{OA}$)
=$\frac{1}{3}$($\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$)
=$\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$,
故选:C.
点评 本题考查了三角形重心的应用及向量的化简与运算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.若命题p:?x0∈R,x02+x0+1<0,则¬p为( )
| A. | ?x∈R,x2+x+1<0 | B. | ?x∈R,x2+x+1>0 | C. | ?x∈R,x2+x+1≥0 | D. | ?x∈R,x2+x+1≥0 |
2.如图为某几何体的三视图,则该几体的体积为( )
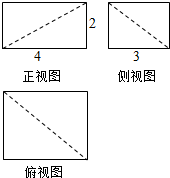

| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
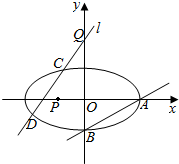 已知椭圆M:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$ (a>b>0)的离心率e=$\frac{\sqrt{6}}{3}$,过点A(a,0)和B(0,-b)的直线与原点的距离为$\frac{\sqrt{3}}{2}$.
已知椭圆M:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$ (a>b>0)的离心率e=$\frac{\sqrt{6}}{3}$,过点A(a,0)和B(0,-b)的直线与原点的距离为$\frac{\sqrt{3}}{2}$.