题目内容
要得到函数y=cos（2x+
）的图象，只须将函数y=cos2x的图象（ ）
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：y=cos2x→y=cos2（x）→y=cos2（x+
），由此可得答案．
| π |
| 6 |
解答：
解：∵y=cos（2x+
）=cos2（x+
），
∴要得到函数y=cos（2x+
）的图象，只须将函数y=cos2x的图象向左平移
个单位．
故选：A．
| π |
| 3 |
| π |
| 6 |
∴要得到函数y=cos（2x+
| π |
| 3 |
| π |
| 6 |
故选：A．
点评：本题考查y=Acos（ωx+φ）型函数的图象变换，关键是明确平移单位是对x而言，不是对ωx，是基础题，也是易错题．
练习册系列答案
相关题目
函数f（x）的定义域为D，满足：①f（x）在D内是单调函数；②存在[
，
]⊆D，使得f（x）在[
，
]上的值域为[a，b]，那么就称函数y=f（x）为“优美函数”，若函数f（x）=logc（cx-t）（c＞0，c≠1）是“优美函数”，则t的取值范围为（ ）
| a |
| 2 |
| b |
| 2 |
| a |
| 2 |
| b |
| 2 |
| A、（0，1） | ||
B、（0，
| ||
C、（-∞，
| ||
D、（0，
|
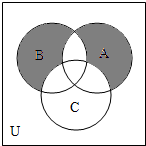如图所示，已知集合A、B、C为全集U的子集，则图中阴影部分所表示的集合为（ ）| A、（∁∪C）∪（A∪B） |
| B、（A∪B）∩[∁∪（A∩B）] |
| C、（A∪B）∩[∁∪（A∩B∩C）] |
| D、{A∩[∁∪（B∪C）]}∪{B∩[∁∪（A∪C）]} |
命题“对任意x∈R，均有x2-2x+5≤0”的否定为（ ）
| A、对任意x∈R，均有x2-2x+5≥0 |
| B、对任意x∉R，均有x2-2x+5≤0 |
| C、存在x∈R，使得x2-2x+5＞0 |
| D、存在x∉R，使得x2-2x+5＞0 |
已知变量x，y满足条件：
，则z=
的取值范围（ ）
|
| y |
| x |
| A、[1，2] | ||||
B、[1，
| ||||
C、[-1，
| ||||
D、[
|
在如图所示的茎叶图中，中位数和众数分别是（ ）
| A、93，92 |
| B、92，93 |
| C、91，93 |
| D、93，93 |
若两个集合A、B是非空集合，则“A∩B=B”是“A∪B=A”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |