题目内容
若函数f（x）=x3-ax2+bx+c的导函数为偶函数，则a的值为（ ）
| A、-1 | B、1 | C、0 | D、2 |
考点：导数的运算
专题：导数的概念及应用
分析：求导数可得f′（x）=3x2-2ax+bx，由二次函数可得x=-
=0，解方程可得．
| -2a |
| 2×3 |
解答：
解：∵f（x）=x3-ax2+bx+c，
∴f′（x）=3x2-2ax+bx，
由偶函数可得对称轴x=-
=0，解得a=0
故选：C
∴f′（x）=3x2-2ax+bx，
由偶函数可得对称轴x=-
| -2a |
| 2×3 |
故选：C
点评：本题考查导数的运算和二次函数的奇偶性，属基础题．
练习册系列答案
相关题目
如图所示，圆O的两弦AB和CD交于点E，EF∥CB，EF交AD的延长线于点F，FG切圆O于点G．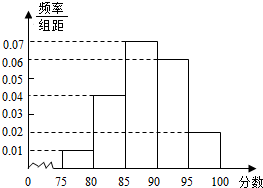
某工厂招聘工人，在一次大型的招聘中，其中1000人的笔试成绩的频率分布直方图如图所示，按厂方规定85分以上（含85分）可以直接录用．在直角三角形ABC中，∠C=
，AC=3，取点D使
=2
，那么
•
=（ ）
| π |
| 2 |
| BD |
| DA |
| CD |
| CA |
| A、3 | B、4 | C、5 | D、6 |