题目内容
求不等式
>
的解集.
| 1 |
| 2x-1 |
| 1 |
| 1-2x-1 |
考点:其他不等式的解法
专题:不等式的解法及应用
分析:作差后化积,结合图形(穿根法),利用对数函数的性质即可求得答案
解答:
解:∵
-
=
=
>0,

由图知1<2x<
或2x>2,
解得0<x<log2
,或x>1.
∴原不等式的解集为{x|0<x<log2
,或x>1}.
| 1 |
| 2x-1 |
| 1 |
| 1-2x-1 |
| 4-3•2x |
| (2x-1)(2-2x) |
| 3•2x-4 |
| (2x-1)(2x-2) |

由图知1<2x<
| 4 |
| 3 |
解得0<x<log2
| 4 |
| 3 |
∴原不等式的解集为{x|0<x<log2
| 4 |
| 3 |
点评:本题考查分式不等式的解法,作差后化积,利用数形结合是解决问题的关键,属于中档题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目

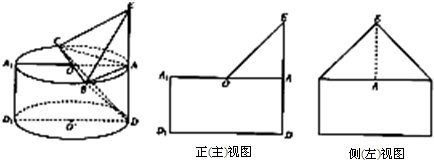
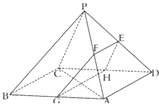 如图,四棱锥P-ABCD中,底面ABCD是边长为2
如图,四棱锥P-ABCD中,底面ABCD是边长为2 如图,已知正方体ABCD-A1B1C1D1的棱长为2,M为正方形AA1D1D的中心,N为棱AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,M为正方形AA1D1D的中心,N为棱AB的中点. 如图,三棱柱ABC-A1B1C1是直棱柱,AB⊥AC,AB=AC=AA1=2,点MN分别为A1B和B1C1的中点.
如图,三棱柱ABC-A1B1C1是直棱柱,AB⊥AC,AB=AC=AA1=2,点MN分别为A1B和B1C1的中点.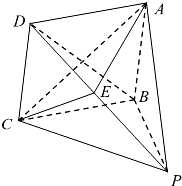 如图,在四棱锥P-ABCD中,底面ABCD为菱形,PB⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,PB⊥平面ABCD.