题目内容
已知等比数列{an}满足:a2=4,公比q=2,数列{bn}的前n项和为Sn,且Sn=
bn-
an+
(n∈N*).
(1)求数列{an}和数列{bn}的通项an和bn;
(2)设Pn=
(n∈N*),证明:
Pi<
.
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
(1)求数列{an}和数列{bn}的通项an和bn;
(2)设Pn=
| an |
| Sn |
| n |
 |
| i=1 |
| 3 |
| 2 |
考点:数列的求和,数列递推式,数列与不等式的综合
专题:等差数列与等比数列
分析:(1)由已知得an=a2•2n-2=2n.所以Sn=
b n-
(2n-1),由此推导出数列{bn+2n}是首项为b1+2=4,公比为4的等比数列,从而求出bn=4n-2n.
(2)由bn=4n-2n,得Pn=
=
=
(
-
),由此能证明
Pi<
.
| 4 |
| 3 |
| 2 |
| 3 |
(2)由bn=4n-2n,得Pn=
| an |
| Sn |
| 2n | ||
|
| 3 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1-1 |
| n |
 |
| i=1 |
| 3 |
| 2 |
解答:
(1)解:由a2=4,q=2得,an=a2•2n-2=2n.(2分)
由上式结合Sn=
b n-
an+
,
得Sn=
b n-
(2n-1),
则当n≥2时,bn=Sn-Sn-1=
bn-
(2n-1)-
bn-1+
(2n-1-1),(4分)
∴bn-2n+1-4bn-1+2n=0,(5分)
∴bn+2n=4(bn-1 +2n-1),(7分)
∵b1=S1=
b1-
×1,∴b1=2,(8分)
∴数列{bn+2n}是首项为b1+2=4,公比为4的等比数列,(9分)
∴bn+2n=4×4n-1=4n,∴bn=4n-2n.(10分)
(2)证明:由bn=4n-2n,
得Sn=
b n-
(2n-1)
=
(4n-2n)-
(2n-1)=
(2n+1-1)(2n-1),
∴Pn=
=
=
(
-
),(12分)
∴
Pi=P1+P2+…+Pn
=
[(1-
)+(
-
)+…+(
-
)
=
(1-
)<
.(14分)
由上式结合Sn=
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
得Sn=
| 4 |
| 3 |
| 2 |
| 3 |
则当n≥2时,bn=Sn-Sn-1=
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
∴bn-2n+1-4bn-1+2n=0,(5分)
∴bn+2n=4(bn-1 +2n-1),(7分)
∵b1=S1=
| 4 |
| 3 |
| 2 |
| 3 |
∴数列{bn+2n}是首项为b1+2=4,公比为4的等比数列,(9分)
∴bn+2n=4×4n-1=4n,∴bn=4n-2n.(10分)
(2)证明:由bn=4n-2n,
得Sn=
| 4 |
| 3 |
| 2 |
| 3 |
=
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
∴Pn=
| an |
| Sn |
| 2n | ||
|
| 3 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1-1 |
∴
| n |
 |
| i=1 |
=
| 3 |
| 2 |
| 1 |
| 22-1 |
| 1 |
| 22-1 |
| 1 |
| 23-1 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1-1 |
=
| 3 |
| 2 |
| 1 |
| 2n+1-1 |
| 3 |
| 2 |
点评:本题考查数列的通项公式的求法,考查不等式的证明,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设f(sinα+cosα)=sin2α,则f(
)的值为( )
| 1 |
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
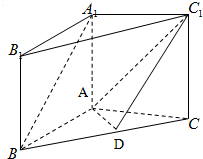 在三棱柱A1B1C1-ABC中,A1A⊥平面ABC,A1A=AB=AC=2,BC=2
在三棱柱A1B1C1-ABC中,A1A⊥平面ABC,A1A=AB=AC=2,BC=2
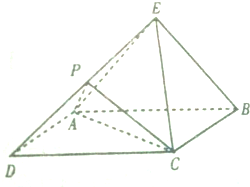 如图,设四棱锥E-ABCD的底面为菱形,且∠ABC=60°,P为DE上一点 若BE∥平面PAC.
如图,设四棱锥E-ABCD的底面为菱形,且∠ABC=60°,P为DE上一点 若BE∥平面PAC.