题目内容
如图,一个几何体是由圆柱OO′和三棱锥E-ABC组合而成,点A、B、C在圆O的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,EA⊥平面ABC,AB⊥AC,AB=AC,AE=2
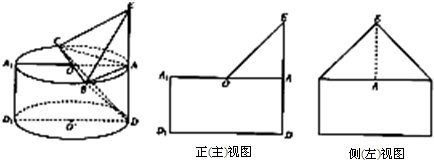
(Ⅰ)求证:AC⊥BD;
(Ⅱ)求O′到平面ABD的距离.

(Ⅰ)求证:AC⊥BD;
(Ⅱ)求O′到平面ABD的距离.
考点:点、线、面间的距离计算,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(Ⅰ)由已知中EA⊥平面ABC,由线面垂直的性质可得ED⊥AC,结合AC⊥AB,由线面垂直的判定定理可得AC⊥平面EBD,再由线面垂直的性质得到AC⊥BD.
(Ⅱ)设圆O的半径为r,圆柱高为h,由已知条件解得
,以D为原点,以DD1为x轴,以过点D在⊙O′所在平面内垂直于DD1的直线为y轴,利用向量法能求出O′到平面ABD的距离.
(Ⅱ)设圆O的半径为r,圆柱高为h,由已知条件解得
|
解答:
(Ⅰ)证明:∵EA⊥平面ABC,AC?平面ABC,
∴EA⊥AC,即ED⊥AC.
又∵AC⊥AB,AB∩ED=A,
∴AC⊥平面EBD.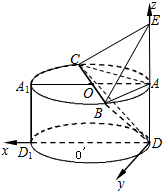
∵BD?平面EBD,∴AC⊥BD.
(Ⅱ)解:∵A、B、C在圆O的圆周上,且AB⊥AC,
∴BC是圆O的直径,
设圆O的半径为r,圆柱高为h,
∵正(主)视图、侧(左)视图的面积分别为10和12,
A⊥平面ABC,AB⊥AC,AB=AC,AE=2,
∴
,解得
,
以D为原点,以DD1为x轴,以过点D在⊙O′所在平面内垂直于DD1的直线为y轴,
以DA为z轴,建立空间直角坐标系,
由(1)知,AC⊥BD,又因为AC⊥AB,AB∩BD=B,
∴AC⊥平面ABD.
∵A(0,0,2),C(2,-2,2),O′(2,0,0),
=(2,-2,0)是平面ABD的一个法向量,
=(2,0,-2),
∴O′到平面ABD的距离d=
=
=
.
∴EA⊥AC,即ED⊥AC.
又∵AC⊥AB,AB∩ED=A,
∴AC⊥平面EBD.

∵BD?平面EBD,∴AC⊥BD.
(Ⅱ)解:∵A、B、C在圆O的圆周上,且AB⊥AC,
∴BC是圆O的直径,
设圆O的半径为r,圆柱高为h,
∵正(主)视图、侧(左)视图的面积分别为10和12,
A⊥平面ABC,AB⊥AC,AB=AC,AE=2,
∴
|
|
以D为原点,以DD1为x轴,以过点D在⊙O′所在平面内垂直于DD1的直线为y轴,
以DA为z轴,建立空间直角坐标系,
由(1)知,AC⊥BD,又因为AC⊥AB,AB∩BD=B,
∴AC⊥平面ABD.
∵A(0,0,2),C(2,-2,2),O′(2,0,0),
| AC |
| AO′ |
∴O′到平面ABD的距离d=
|
| ||||
|
|
| |4| | ||
2
|
| 2 |
点评:本题考查的知识点是由几何体的结构特征得到线线垂直,进而建立空间坐标系,利用向量法求解点到平面的距离.

练习册系列答案
相关题目
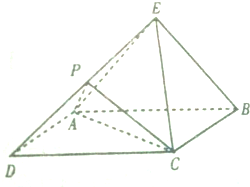 如图,设四棱锥E-ABCD的底面为菱形,且∠ABC=60°,P为DE上一点 若BE∥平面PAC.
如图,设四棱锥E-ABCD的底面为菱形,且∠ABC=60°,P为DE上一点 若BE∥平面PAC.