题目内容
设3a=2，3b=6，3c=18，则a、b、c是（ ）
| A、等差数列 |
| B、每项倒数成等差数列 |
| C、每项的平方成等差数列 |
| D、每项立方成等差数列 |
考点：指数式与对数式的互化
专题：等差数列与等比数列
分析：根据指数幂和对数之间的关系，结合等差数列和等比数列的定义即可得到结论．
解答：
解：∵3a=2，3b=6，3c=18，2×18=62，
∴3a•3c=（3b）2，
即a+c=2b，
则a，b，c成等差数列，
故选：A．
∴3a•3c=（3b）2，
即a+c=2b，
则a，b，c成等差数列，
故选：A．
点评：本题主要考查等差数列的判断，利用指数幂的运算法则是解决本题的关键，比较基础．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
如果复数z满足条件z+|z|=3+i，那么z等于（ ）
A、
| ||
B、-
| ||
C、-
| ||
D、
|
已知sin（π+α）=
，则cos（
-α）=（ ）
| 1 |
| 3 |
| 3π |
| 2 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
在△ABC中，角A，B，C所对的边分别为5，7，8，则∠B的大小是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f（x）=ax2+x+1有极大值的充要条件是（ ）
| A、a＜0 | B、a≥0 |
| C、a＞0 | D、a≤0 |
若点A（1，m-1，1）和点B（-1，-3，-1）关于原点对称，则m=（ ）
| A、-4 | B、4 | C、2 | D、-2 |
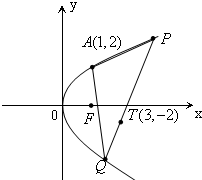点A（1，2）到抛物线y2=2px（p＞0）的焦点F的距离为2，过T（3，-2）的动直线l与此抛物线交于P、Q两点