题目内容
已知椭圆E:
+
=1(a>b>c)的离心率为
,且经过点P(1,
)
(Ⅰ)求椭圆E的方程;
(Ⅱ)设直线x=my+1交椭圆E于A,B两点,射线OA,OB分别交直线l:x=2于M,N,记△OAB,△OMN的面积分别为S1,S2,λ=
,当m∈[
,
]时,求λ的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
(Ⅰ)求椭圆E的方程;
(Ⅱ)设直线x=my+1交椭圆E于A,B两点,射线OA,OB分别交直线l:x=2于M,N,记△OAB,△OMN的面积分别为S1,S2,λ=
| S2 |
| S1 |
| 1 |
| 2 |
| ||
| 2 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件推导出
,由此能求出椭圆E的方程.
(Ⅱ)设A(my1+1,y1),B(my2+1,y2),M(xM,yM),N(xN,yN),OA的方程为y=
x,OB的方程为y=
x,由此求出|MN|=|
|,由
,得|y1-y2|=
,从而得到|MN|=
,|AB|=
|y1-y2|=
,由此能求出λ的取值范围.
|
(Ⅱ)设A(my1+1,y1),B(my2+1,y2),M(xM,yM),N(xN,yN),OA的方程为y=
| y1 |
| my1+1 |
| y2 |
| my2+1 |
| 2(y1-y2) |
| m2y1y2+m(y1+y2)+1 |
|
2
| ||||
| m2+2 |
2
| ||||
| |m2-1| |
| 1+m2 |
2
| ||
| m2+2 |
解答:
解:(Ⅰ)∵椭圆E:
+
=1(a>b>c)的离心率为
,且经过点P(1,
),
∴
,解得
,
∴椭圆E的方程为
+y2=1.
(Ⅱ)设A(my1+1,y1),B(my2+1,y2),M(xM,yM),N(xN,yN),
∴OA的方程为y=
x,OB的方程为y=
x,
由
,解得yM=
,
同理求得yN=
,
∴|MN|=|yM-yN|=|
|,①
由
,得(m2+2)y2+2my-1=0,
∴△=4m2+4(m2+2)>0,
y1+y2=-
,y1y2=-
,|y1-y2|=
,②
将②代入①,整理,得:
|MN|=
,又|AB|=
|y1-y2|=
,
设点O到直线AB,l的距离分别为d1,d2,
则d1=
,d2=2,
∴S1=
|AB|d1=
,
S2=
|MN|d2=
,
∴λ=
=2•|
|=2|1+
|,
∵m∈[
,
],∴λ∈[6,10],
∴λ的取值范围是[6,10].
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
∴
|
|
∴椭圆E的方程为
| x2 |
| 2 |
(Ⅱ)设A(my1+1,y1),B(my2+1,y2),M(xM,yM),N(xN,yN),
∴OA的方程为y=
| y1 |
| my1+1 |
| y2 |
| my2+1 |
由
|
| 2y1 |
| my1+1 |
同理求得yN=
| 2y2 |
| my2+1 |
∴|MN|=|yM-yN|=|
| 2(y1-y2) |
| m2y1y2+m(y1+y2)+1 |
由
|
∴△=4m2+4(m2+2)>0,
y1+y2=-
| 2m |
| m2+2 |
| 1 |
| m2+2 |
2
| ||||
| m2+2 |
将②代入①,整理,得:
|MN|=
2
| ||||
| |m2-1| |
| 1+m2 |
2
| ||
| m2+2 |
设点O到直线AB,l的距离分别为d1,d2,
则d1=
| 1 | ||
|
∴S1=
| 1 |
| 2 |
| ||||
| m2+2 |
S2=
| 1 |
| 2 |
2
| ||||
| |m2-1| |
∴λ=
| S2 |
| S1 |
| m2+2 |
| m2-1 |
| 3 |
| m2-1 |
∵m∈[
| 1 |
| 2 |
| ||
| 2 |
∴λ的取值范围是[6,10].
点评:本题考查椭圆方程的求法,考查实数的取值范围的求法,解题时要认真审题,注意函数与方程思想、等价转化思想的合理运用.

练习册系列答案
相关题目
设3a=2,3b=6,3c=18,则a、b、c是( )
| A、等差数列 |
| B、每项倒数成等差数列 |
| C、每项的平方成等差数列 |
| D、每项立方成等差数列 |
 如图,设A是单位圆和x轴正半轴的交点,P,Q是单位圆上两点,O是坐标原点,且P(
如图,设A是单位圆和x轴正半轴的交点,P,Q是单位圆上两点,O是坐标原点,且P( 如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.
如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.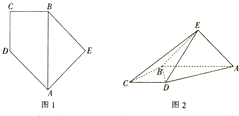 已知直角梯形ABCD的下底与等腰直角三角形ABE的斜边重合,AB⊥BC,且AB=2CD=2BC(如图1),将此图形沿AB折叠成直二面角,连接EC、ED,得到四棱锥E-ABCD(如图2).
已知直角梯形ABCD的下底与等腰直角三角形ABE的斜边重合,AB⊥BC,且AB=2CD=2BC(如图1),将此图形沿AB折叠成直二面角,连接EC、ED,得到四棱锥E-ABCD(如图2).