题目内容
关于x不等式log
(
+1)•log5(x2+ax+6)+loga3≥0解集为单元素集,求实数a的取值范围.
| 1 |
| a |
| x2+ax+5 |
考点:其他不等式的解法
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:对a讨论,a>1和0<a<1两种情况,运用对数的换底公式,全部以a为底,运用对数函数的单调性,及换元法,令f(t)=loga(t+1)•loga(1+t2)-loga3•loga5,判断单调性,再由二次不等式的解法与判别式的关系,即可得到所求范围.
解答:
解:①当a>1时,log
(
+1)•log5(x2+ax+6)+loga3≥0
即为-loga(
+1)•log5(x2+ax+6)+loga3≥0,
令
=t(t≥0),则-loga(t+1)•log5(1+t2)+loga3≥0,
由于loga3>0,loga5>0,
则有loga(t+1)•loga(1+t2)-loga3•loga5≤0,
令f(t)=loga(t+1)•loga(1+t2)-loga3•loga5,则f(t)递增,
且f(2)=0,即有f(t)≤f(2),即有t≤2.
即有0≤x2+ax+5≤4,由于只有一解,则判别式a2-4=0,解得,a=2;
②当0<a<1时,log
(
+1)•log5(x2+ax+6)+loga3≥0
即为-loga(
+1)•log5(x2+ax+6)+loga3≥0,
令
=t(t≥0),则-loga(t+1)•log5(1+t2)+loga3≥0,
由于loga3<0,loga5<0,
则有loga(t+1)•loga(1+t2)-loga3•loga5≥0,
令f(t)=loga(t+1)•loga(1+t2)-loga3•loga5,则f(t)递减,
且f(2)=0,即有f(t)≥f(2),即有t≤2.
即有x2+ax+5≤4,由于判别式a2-4<0,则不等式的解集为∅.
综上可得,a的取值范围为{2}.
| 1 |
| a |
| x2+ax+5 |
即为-loga(
| x2+ax+5 |
令
| x2+ax+5 |
由于loga3>0,loga5>0,
则有loga(t+1)•loga(1+t2)-loga3•loga5≤0,
令f(t)=loga(t+1)•loga(1+t2)-loga3•loga5,则f(t)递增,
且f(2)=0,即有f(t)≤f(2),即有t≤2.
即有0≤x2+ax+5≤4,由于只有一解,则判别式a2-4=0,解得,a=2;
②当0<a<1时,log
| 1 |
| a |
| x2+ax+5 |
即为-loga(
| x2+ax+5 |
令
| x2+ax+5 |
由于loga3<0,loga5<0,
则有loga(t+1)•loga(1+t2)-loga3•loga5≥0,
令f(t)=loga(t+1)•loga(1+t2)-loga3•loga5,则f(t)递减,
且f(2)=0,即有f(t)≥f(2),即有t≤2.
即有x2+ax+5≤4,由于判别式a2-4<0,则不等式的解集为∅.
综上可得,a的取值范围为{2}.
点评:本题考查对数不等式的解法,考查对数函数的单调性和运用,考查分类讨论的思想方法,考查运算化简能力,属于中档题和易错题.

练习册系列答案
相关题目
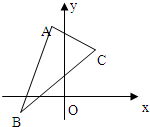 如图,已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3)
如图,已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3) 如图,已知圆柱体底面圆的半径为
如图,已知圆柱体底面圆的半径为