题目内容
函数f（x）=ln（1+x）+
的定义域为（ ）
| ||
| x |
| A、（-1，0）∪（0，1] |
| B、（-1，1） |
| C、（-1，1] |
| D、[-1，0）∪（0，1] |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据对数函数和二次根式的性质，要使函数有意义，则需真数大于零且被开方式非负．
解答：
解：由函数f（x）=ln（1+x）+
得
，
解得-1＜x＜0或0＜x≤1．
则定义域为（-1，0）∪（0，1]．
故选：A．
| ||
| x |
|
解得-1＜x＜0或0＜x≤1．
则定义域为（-1，0）∪（0，1]．
故选：A．
点评：本题主要考查对数函数和二次根式的定义域，基本求法是真数大于零且被开方式非负．要注意定义域要写成集合或区间的形式．
练习册系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
等比数列{an}的前n项和为Sn，已知a2a3=2a1，且a4与2a7的等差中项为
，则S5=（ ）
| 5 |
| 4 |
| A、29 | B、31 | C、33 | D、36 |
设集合A={x||x-1|≤2}，B={x|log2x＜2}，则A∪B=（ ）
| A、[-1，3] |
| B、[-1，4） |
| C、（0，3] |
| D、（-∞，4） |
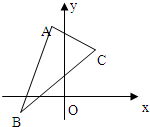如图，已知△ABC三个顶点是A（-1，4），B（-2，-1），C（2，3）