题目内容
tan(α+45°)-tan(45°-α)等于.
| A、2tan2α | ||
| B、-2tan2α | ||
C、
| ||
D、-
|
考点:两角和与差的正切函数
专题:三角函数的求值
分析:利用两角和与差的正切函数公式化简后通分,由二倍角的正切公式即可化简.
解答:
解:tan(α+45°)-tan(45°-α)=
-
=
=
=2tan2α.
故选:A.
| 1+tanα |
| 1-tanα |
| 1-tanα |
| 1+tanα |
| (1+tanα)2-(1-tanα)2 |
| 1-tan2α |
| 4tanα |
| 1-tan2α |
故选:A.
点评:本题主要考查了两角和与差的正切函数公式,二倍角的正切公式的应用,属于基础题.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
函数f(x)=
+
的定义域是( )
| 3x2 | ||
|
| 3x+1 |
A、(-
| ||
B、(-
| ||
C、[-
| ||
| D、[0,1) |
设a=tan35°,b=cos55°,c=sin23°,则( )
| A、a>b>c |
| B、b>c>a |
| C、c>b>a |
| D、c>a>b |
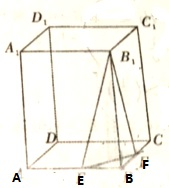 已知正四棱柱ABCD-A1B1C1D1,其底面边长为4,高为
已知正四棱柱ABCD-A1B1C1D1,其底面边长为4,高为