题目内容
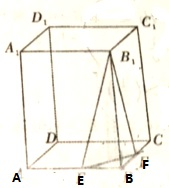 已知正四棱柱ABCD-A1B1C1D1,其底面边长为4,高为
已知正四棱柱ABCD-A1B1C1D1,其底面边长为4,高为| 6 |
(1)求二面角B-EF-B1的大小;
(2)求VB1-BEF.
考点:棱柱、棱锥、棱台的体积,二面角的平面角及求法
专题:空间位置关系与距离
分析:(1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,由此能求出二面角B-EF-B1的大小.
(2)由VB1-BEF=
×S△BEF×BB1,能求出结果.
(2)由VB1-BEF=
| 1 |
| 3 |
解答:
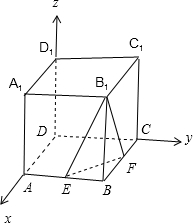 解:(1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,
解:(1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,
建立空间直角坐标系,
B(4,4,0),E(4,2,0),
F(2,4,0),B1(4,4,
),
=(-2,2,0),
=(0,2,
),
设平面B1EF的法向量
=(x,y,z),
则
,
取z=
,得
=(-3,-3,
),
又平面BEF的法向量
=(0,0,1),
cos<
,
>=
=
,
∴<
,
>=60°,
∴二面角B-EF-B1的大小为60°.
(2)VB1-BEF=
×S△BEF×BB1
=
×
×2×2×
=
.
 解:(1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,
解:(1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
B(4,4,0),E(4,2,0),
F(2,4,0),B1(4,4,
| 6 |
| EF |
| EB1 |
| 6 |
设平面B1EF的法向量
| n |
则
|
取z=
| 6 |
| n |
| 6 |
又平面BEF的法向量
| m |
cos<
| n |
| m |
| ||
|
| 1 |
| 2 |
∴<
| n |
| m |
∴二面角B-EF-B1的大小为60°.
(2)VB1-BEF=
| 1 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| 6 |
2
| ||
| 3 |
点评:本题考查二面角的大小的求法,考查三棱锥的体积的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
tan(α+45°)-tan(45°-α)等于.
| A、2tan2α | ||
| B、-2tan2α | ||
C、
| ||
D、-
|
直线l:3x+4y-25=0与圆C:x2+y2-6x-8y=0的位置关系是( )
| A、相离 | B、相切 |
| C、相交且过圆心 | D、相交但不过圆心 |
 正方体ABCD-A1B1C1D1的棱长为1,底面ABCD内任一点M,作MN⊥BC,垂足为N,满足条件|A1M|2-|MN|2=1.则点M的轨迹为( )
正方体ABCD-A1B1C1D1的棱长为1,底面ABCD内任一点M,作MN⊥BC,垂足为N,满足条件|A1M|2-|MN|2=1.则点M的轨迹为( )| A、线段 |
| B、椭圆的一部分 |
| C、双曲线的一部分 |
| D、抛物线的一部分 |
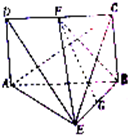 如图,已知四棱锥E-ABCD的底面ABCD是平行四边形,AE⊥BE,平面ACE⊥平面BCE,
如图,已知四棱锥E-ABCD的底面ABCD是平行四边形,AE⊥BE,平面ACE⊥平面BCE,