题目内容
5.已知斜率为1的直线l经过抛物线y2=2px(p>0)的焦点F,且与抛物线相交于A,B两点,|AB|=4.(I)求p的值;
(II)若经过点D(-2,-1),斜率为k的直线m与抛物线有两个不同的公共点,求k的取值范围.
分析 (I)由$\left\{\begin{array}{l}y=x-\frac{p}{2}\\{y^2}=2px\end{array}\right.$消y并整理,利用|AB|=|AF|+|BF|=x1+x2+p=4,即可求p的值;
(II)由题意,直线m的方程为y=kx+(2k-1),与抛物线方程联立,利用判别式,即可求k的取值范围.
解答 解:(I)由题意可知,抛物线y2=2px(p>0)的焦点坐标为$F(\frac{p}{2},0)$,准线方程为$x=-\frac{p}{2}$.
所以,直线l的方程为$y=x-\frac{p}{2}$…(2分)
由$\left\{\begin{array}{l}y=x-\frac{p}{2}\\{y^2}=2px\end{array}\right.$消y并整理,得${x^2}-3px+\frac{p^2}{4}=0$…(3分)
设A(x1,y1),B(x2,y2)
则x1+x2=3p,
又|AB|=|AF|+|BF|=x1+x2+p=4,
所以,3p+p=4,所以p=1…(6分)
(II)由(I)可知,抛物线的方程为y2=2x.
由题意,直线m的方程为y=kx+(2k-1).…(7分)
由方程组$\left\{\begin{array}{l}y=kx+(2k-1)\\{y^2}=2x\end{array}\right.$(1)
可得ky2-2y+4k-2=0(2)…(8分)
当k=0时,由方程(2),得y=-1.
把y=-1代入y2=2x,得$x=\frac{1}{2}$.
这时.直线m与抛物线只有一个公共点$(\frac{1}{2},-1)$.…(9分)
当k≠0时,方程(2)得判别式为△=4-4k(4k-2).
由△>0,即4-4k(4k-2)>0,亦即4k2-2k-1<0.
解得$\frac{{1-\sqrt{5}}}{4}<k<\frac{{1+\sqrt{5}}}{4}$.
于是,当$\frac{{1-\sqrt{5}}}{4}<k<\frac{{1+\sqrt{5}}}{4}$且k≠0时,方程(2)有两个不同的实根,从而方程组(1)有两组不同的解,这时,直线m与抛物线有两个不同的公共点,…(12分)
因此,所求m的取值范围是$(\frac{{1-\sqrt{5}}}{4},0)∪(0,\frac{{1+\sqrt{5}}}{4})$.…(13分)
点评 本题考查抛物线的方程与性质,考查直线与抛物线的位置关系,考查学生分析解决问题的能力,属于中档题.

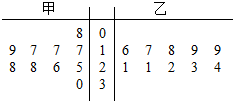 某校为了解高三学生英语听力情况,抽查了甲、乙两班各十名学生的一次英语听力成绩,并将所得数据用茎叶图表示(如图所示),则以下判断正确的是( )
某校为了解高三学生英语听力情况,抽查了甲、乙两班各十名学生的一次英语听力成绩,并将所得数据用茎叶图表示(如图所示),则以下判断正确的是( )| A. | 甲组数据的众数为28 | B. | 甲组数据的中位数是22 | ||
| C. | 乙组数据的最大值为30 | D. | 乙组数据的极差为16 |
| x(万元) | 2 | 3 | 4.5 | 5 | 7.5 | 8 |
| y(吨) | 3 | 3.5 | 3.5 | 4 | 6 | 7 |
(Ⅱ)已知这种产品的年利润z(单位:万元)与x、y之间的关系为z=30y-x2,根据(Ⅰ)中所求的回归方程,求年宣传费x为何值时,年利润z的预估值最大?
| A. | 命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” | |
| B. | 若命题p:“?x∈R,x2-x-1>0”,则命题p的否定为“?x∈R,x2-x-1≤0” | |
| C. | “x=1”是“x2+5x-6=0”的充分不必要条件 | |
| D. | “a=1”是“直线x-ay=0与直线x+ay=0互为垂直”的充要条件 |
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{\sqrt{5}}{3}$ | D. | -$\frac{\sqrt{5}}{3}$ |
 函数f(x)的图象为如图所示的折线段ABC,设g(x)=$\frac{lo{g}_{3}x}{f(x)}$,则函数g(x)的最大值为( )
函数f(x)的图象为如图所示的折线段ABC,设g(x)=$\frac{lo{g}_{3}x}{f(x)}$,则函数g(x)的最大值为( )