题目内容
16.把正整数排列成如图甲所示三角形数阵,然后擦去偶数行中的奇数和奇数行中的偶数,得到如图乙所示三角形数阵,设aij为图乙三角形数阵中第i行第j个数,若amn=2015,则实数对(m,n)为(45,40).
分析 观察图乙找出每行数字的规律,即可使用数列知识解出.
解答 解:观察图乙可发现以下规律:
(1)第一行有1个数字,第二行有2个数字,第三行有3个数字,…故可归纳得出第i行有i个数字;
(2)每一行的数字从左到右都是等差为2的等差数列;
(3)每一行的第一个数字都比上一行的最后一个数字大1;
(4)每一行的最后一个数字都是该行数的平方.
∵442=1936<2015,452=2025>2015,∴2015是第45行的数字,
设第45行第n个数字为an,则a1=1937,d=2,∴an=1937+2(n-1)=2n+1935.
令an=2n+1935=2015,解得n=40.
∴2015是第45行第40个数字,
故答案为(45,40).
点评 本题考查了归纳推理,寻找图中数字的规律是解题的关键.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
6.已知点A(5,0),抛物线C:y2=4x的焦点为F,点P在抛物线C上,若点F恰好在PA的垂直平分线上,则PA的长度为( )
| A. | 2 | B. | $2\sqrt{2}$ | C. | 3 | D. | 4 |
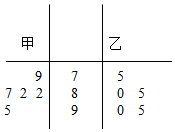 甲、乙两位学生参加某项竞赛培训,在培训期间,他们参加的5项预赛成绩的茎叶图记录如下:
甲、乙两位学生参加某项竞赛培训,在培训期间,他们参加的5项预赛成绩的茎叶图记录如下: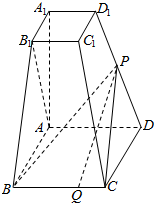 已知四棱台ABCD-A1B1C1D1的上下底面分别是边长为2和4的正方形,AA1=4且AA1⊥底面ABCD,点P为DD1的中点,Q为BC边上的一点.
已知四棱台ABCD-A1B1C1D1的上下底面分别是边长为2和4的正方形,AA1=4且AA1⊥底面ABCD,点P为DD1的中点,Q为BC边上的一点.