题目内容
15. 函数f(x)的图象为如图所示的折线段ABC,设g(x)=$\frac{lo{g}_{3}x}{f(x)}$,则函数g(x)的最大值为( )
函数f(x)的图象为如图所示的折线段ABC,设g(x)=$\frac{lo{g}_{3}x}{f(x)}$,则函数g(x)的最大值为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 运用一次函数的解析式的求法,可得f(x),分别讨论0<x≤1,1<x≤3时,f(x)和g(x)的单调性,即可得到所求最大值.
解答 解:由图象可得A(0,1),B(1,3),C(3,1),
即有f(x)=$\left\{\begin{array}{l}{2x+1,0<x≤1}\\{4-x,1<x≤3}\end{array}\right.$,
当0<x≤1时,g(x)=$\frac{lo{g}_{3}x}{2x+1}$≤0,
x=1时,取得最大值0;
当1<x≤3时,g(x)=$\frac{lo{g}_{3}x}{4-x}$递增,
当x=3时,取得最大值$\frac{lo{g}_{3}3}{4-3}$=1.
综上可得,g(x)的最大值为1.
故选B.
点评 本题考查分段函数的解析式的求法,主要考查函数的最值的求法,注意运用对数函数的单调性和一次函数的单调性,考查运算能力,属于中档题.

练习册系列答案
相关题目
6.已知点A(5,0),抛物线C:y2=4x的焦点为F,点P在抛物线C上,若点F恰好在PA的垂直平分线上,则PA的长度为( )
| A. | 2 | B. | $2\sqrt{2}$ | C. | 3 | D. | 4 |
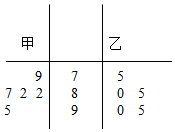 甲、乙两位学生参加某项竞赛培训,在培训期间,他们参加的5项预赛成绩的茎叶图记录如下:
甲、乙两位学生参加某项竞赛培训,在培训期间,他们参加的5项预赛成绩的茎叶图记录如下: