题目内容
函数y=1-
cos（2x+
）的最大值是 ．
| 1 |
| 2 |
| π |
| 3 |
考点：余弦函数的定义域和值域
专题：三角函数的图像与性质
分析：由三角形的有界性可知当cos（2x+
）=-1时，函数取最大值．
| π |
| 3 |
解答：
解：由题意可知cos（2x+
）∈[-1，1]，
∴当cos（2x+
）=-1时，
函数取最大值ymax=1-
×（-1）=
故答案为：
．
| π |
| 3 |
∴当cos（2x+
| π |
| 3 |
函数取最大值ymax=1-
| 1 |
| 2 |
| 3 |
| 2 |
故答案为：
| 3 |
| 2 |
点评：本题考查余弦函数的值域，属基础题．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
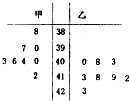为调查甲乙两人网站受欢迎的程度，随机选取了某个月1号至8号，统计这8天内每天同一时间段的点击量，得到如图所示的茎叶图．
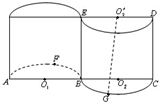如图所示的几何体，是将高为2、底面半径为1的圆柱沿过旋转轴的平面切开后，将其中一半沿切面向右水平平移后形成的封闭体．O1，O2，O2′分别为AB，BC，DE的中点，F为弧AB的中点，G为弧BC的中点．则异面直线AF与GO2′所成的角的余弦值为（文科）在△ABC中，如果sinA：sinB：sinC=2：3：4，那么最大角的余弦值等于（ ）
A、
| ||
B、-
| ||
C、-
| ||
D、-
|