题目内容
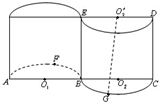 如图所示的几何体,是将高为2、底面半径为1的圆柱沿过旋转轴的平面切开后,将其中一半沿切面向右水平平移后形成的封闭体.O1,O2,O2′分别为AB,BC,DE的中点,F为弧AB的中点,G为弧BC的中点.则异面直线AF与GO2′所成的角的余弦值为
如图所示的几何体,是将高为2、底面半径为1的圆柱沿过旋转轴的平面切开后,将其中一半沿切面向右水平平移后形成的封闭体.O1,O2,O2′分别为AB,BC,DE的中点,F为弧AB的中点,G为弧BC的中点.则异面直线AF与GO2′所成的角的余弦值为考点:异面直线及其所成的角
专题:空间角
分析:连接AF、FB、BG、GC,由圆的性质可知,G、B、F三点共线,且△AFB≌△CGB,可得AF∥CG,则∠CGO2′即为所求的角或其补角,然后利用余弦定理在三角形CGO2′求解即可.
解答:
 解:如图,连接AF、FB、BG、GC,∵F为半圆弧AFB的中点,G为半圆弧BGC的中点,
解:如图,连接AF、FB、BG、GC,∵F为半圆弧AFB的中点,G为半圆弧BGC的中点,
由圆的性质可知,G、B、F三点共线,且AF=CG,FB=GB,AB=BC,
∴△AFB≌△CGB,∴AF∥CG,则∠CGO2′即为所求的角或其补角,
又∵半径为1,高为2,且△AFB,△CGB都是等腰Rt△,
∴CG=
,CO2′=GO2′=
=
,
∴在△CGO2′中,cos∠CGO2′=
=
,
即异面直线AF与GO2′所成的角余弦值
.
故答案为:
.
 解:如图,连接AF、FB、BG、GC,∵F为半圆弧AFB的中点,G为半圆弧BGC的中点,
解:如图,连接AF、FB、BG、GC,∵F为半圆弧AFB的中点,G为半圆弧BGC的中点,由圆的性质可知,G、B、F三点共线,且AF=CG,FB=GB,AB=BC,
∴△AFB≌△CGB,∴AF∥CG,则∠CGO2′即为所求的角或其补角,
又∵半径为1,高为2,且△AFB,△CGB都是等腰Rt△,
∴CG=
| 2 |
| 1+22 |
| 5 |
∴在△CGO2′中,cos∠CGO2′=
| ||||||
2
|
| ||
| 10 |
即异面直线AF与GO2′所成的角余弦值
| ||
| 10 |
故答案为:
| ||
| 10 |
点评:这个题有些打破传统,是利用圆的性质来完成异面直线所成的角向相交直线所成角的转化,然后在三角形中利用余弦定理求角.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
 已知一个样本容量为100的样本数据的频率分布直方图如图所示,那么样本数据落在[40,60)内的样本的频数为
已知一个样本容量为100的样本数据的频率分布直方图如图所示,那么样本数据落在[40,60)内的样本的频数为