题目内容
9.已知函数f(x)=x3-3ax-1,(a≠0).(1)求f(x)的单调区间;
(2)若f(x)在x=-1处取得极值,直线y=m与y=f(x)的图象有且只有一个交点,求m的取值范围.
分析 (1)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(2)求出函数的导数,计算f′(-1)=3,求出a的值,关键函数的单调性求出函数的极值,画出函数的图象,从而求出m的范围即可.
解答 解:(1)f′(x)=3x2-3a=3(x2-a),
当a<0时,对x∈R,有f′(x)>0,
∴当a<0时,f(x)的单调增区间为(-∞,+∞);
当a>0时,由f′(x)>0,解得x<-$\sqrt{a}$或x>$\sqrt{a}$.
由f′(x)<0,解得-$\sqrt{a}$<x<$\sqrt{a}$,
∴当a>0时,f(x)的单调增区间为(-∞,-$\sqrt{a}$),($\sqrt{a}$,+∞),单调减区间为(-$\sqrt{a}$,$\sqrt{a}$).
(2)∵f(x)在x=-1处取得极值,
∴f′(-1)=3(-1)2-3a=0,∴a=1.
∴f(x)=x3-3x-1,f′(x)=3x2-3,
由f′(x)=0,解得x1=-1,x2=1.
由(1)中f(x)的单调性可知,
f(x)在x=-1处取得极大值f(-1)=1,
在x=1处取得极小值f(1)=-3,
∵直线y=m与函数y=f(x)的图象有三个不同的交点,
结合如图所示f(x)的图象可知: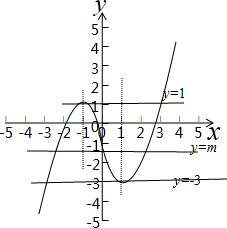
实数m的取值范围是(-∞,-3)∪(1,+∞).
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及数形结合思想,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.过点A(1,0)和B(2,1)的直线的倾斜角为( )
| A. | 30° | B. | 45° | C. | 135° | D. | 150° |
19.已知AB是经过抛物线y2=2px的焦点的弦,若点A、B的横坐标分别为1和$\frac{1}{4}$,则该抛物线的准线方程为( )
| A. | x=1 | B. | x=-1 | C. | x=$\frac{1}{2}$ | D. | x=-$\frac{1}{2}$ |
1.已知函数f(x)=$\left\{\begin{array}{l}{x^2}+1,x≤0\\-x+1,x>0\end{array}$,若a=f(${log_2}\frac{1}{3}$),b=f(${2^{\frac{1}{3}}}$),c=f(${3^{-\frac{1}{2}}}$),则( )
| A. | a>b>c | B. | c>b>a | C. | a>c>b | D. | b>c>a |
19.下列各式中,最小的是( )
| A. | 2cos240°-1 | B. | 2sin6°cos6° | ||
| C. | sin50°cos37°-sin40°cos53° | D. | $\frac{\sqrt{3}}{2}$sin41°-$\frac{1}{2}$cos41° |
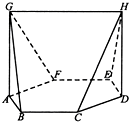 如图,在七面体ABCDEFGH中,底面ABCDEF是边长为2的正六边形,AG=DH=3,且
如图,在七面体ABCDEFGH中,底面ABCDEF是边长为2的正六边形,AG=DH=3,且