题目内容
1.已知函数f(x)=$\left\{\begin{array}{l}{x^2}+1,x≤0\\-x+1,x>0\end{array}$,若a=f(${log_2}\frac{1}{3}$),b=f(${2^{\frac{1}{3}}}$),c=f(${3^{-\frac{1}{2}}}$),则( )| A. | a>b>c | B. | c>b>a | C. | a>c>b | D. | b>c>a |
分析 函数f(x)=$\left\{\begin{array}{l}{x^2}+1,x≤0\\-x+1,x>0\end{array}$在R上减函数,比较三个自变量的大小,可得答案.
解答 解:函数f(x)=$\left\{\begin{array}{l}{x^2}+1,x≤0\\-x+1,x>0\end{array}$在R上减函数,
∵${log_2}\frac{1}{3}$∈(-∞,0),${2^{\frac{1}{3}}}$∈(1,+∞),${3^{-\frac{1}{2}}}$∈(0,1),
∴a>c>b,
故选:C.
点评 本题考查的知识点是分段函数的应用,函数的单调性,指数函数和对数函数的图象和性质,难度中档.

练习册系列答案
相关题目
11.学习雷锋精神前半年内某单位餐厅的固定餐椅经常有损坏,学习雷锋精神时全修好;单位对学习雷锋精神前后各半年内餐椅的损坏情况作了一个大致统计,具体数据如表:
(1)求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
(2)请说明是否有97.5%以上的把握认为损毁餐椅数量与学习雷锋精神有关?
| 损坏餐椅数 | 未损坏餐椅数 | 总 计 | |
| 学习雷锋精神前 | 50 | 150 | 200 |
| 学习雷锋精神后 | 30 | 170 | 200 |
| 总 计 | 80 | 320 | 400 |
(2)请说明是否有97.5%以上的把握认为损毁餐椅数量与学习雷锋精神有关?
16.已知函数f(x)=ax3+2x2-1有且只有两个零点,则实数a的取值集合( )
| A. | {-1,0,1} | B. | {0,$\frac{4\sqrt{6}}{9}$} | C. | {0,$\frac{2\sqrt{3}}{3}$} | D. | {-$\frac{4\sqrt{6}}{9}$,0,$\frac{4\sqrt{6}}{9}$} |
11.设集合A={x|x2-4x+3=0},B={x|x2-5x+4=0},集合A∪B为( )
| A. | {1} | B. | {1,3} | C. | {1,4} | D. | {1,3,4} |
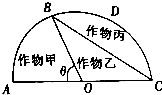 某农场有一块以O为圆心,R(R为常数,单位为米)为半径的半圆形(如图)种植地,农场主计划对其合理利用,其中扇形AOB区域用于种植作物甲出售,△BOC区域用于种植作物乙出售,其余区域用于种植作物丙不出售,已知种植作物甲的利润是40元/平方米;种植作物乙的利润是80元/平方米;种植作物丙的成本是20元/平方米.
某农场有一块以O为圆心,R(R为常数,单位为米)为半径的半圆形(如图)种植地,农场主计划对其合理利用,其中扇形AOB区域用于种植作物甲出售,△BOC区域用于种植作物乙出售,其余区域用于种植作物丙不出售,已知种植作物甲的利润是40元/平方米;种植作物乙的利润是80元/平方米;种植作物丙的成本是20元/平方米.