题目内容
4.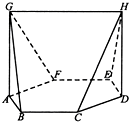 如图,在七面体ABCDEFGH中,底面ABCDEF是边长为2的正六边形,AG=DH=3,且
如图,在七面体ABCDEFGH中,底面ABCDEF是边长为2的正六边形,AG=DH=3,且AG,DH都与底面ABCDEF垂直.
(Ⅰ)求证:平面ABG∥平面DEH;
(Ⅱ)平面BCHG与平面DEH所成二面角的正弦值.
分析 (Ⅰ)由线面垂直的性质可知AG∥平面DEH,由ABCDEF是正六边形,AB∥DE,根据线面平行的性质即可证明平面ABG∥平面DEH;
(Ⅱ)由题意建立空间直角坐标系,分别求得B,C,G点坐标,求得向量$\overrightarrow{BC}$和$\overrightarrow{BG}$,分别求得平面BCHG与平面DEH的法向量,由cos<$\overrightarrow{j}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{j}•\overrightarrow{n}}{丨\overrightarrow{j}丨丨\overrightarrow{n}丨}$,根据同角三角三角函数的基本关系,即可求得平面BCHG与平面DEH所成二面角的正弦值.
解答 证明:(Ⅰ)AG⊥平面ABCDEF垂直,DH⊥ABCDEF垂直.
∴AG∥DH,DH?平面DEH,AG?平面DEH,
∴AG∥平面DEH,
∵ABCDEF是正六边形,
所以AB∥DE,DE?平面DEH,AB?平面DEH,
∴AB相交于A点,
∴平面ABG∥平面DEH;
解:(Ⅱ)连接AE,AE⊥AB,
AG⊥平面ABCDEF,
AB,AE,AG所在直线分别为x,y,z轴,建立坐标系,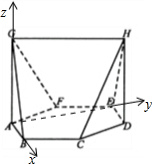
则:B(2,0,0),C(3,$\sqrt{3}$,0),G(0,0,3),
$\overrightarrow{BC}$=(1,$\sqrt{3}$,0),$\overrightarrow{BG}$=(-2,0,3),
设平面BCHG的法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{x+\sqrt{3}y=0}\\{-2x+3z=0}\end{array}\right.$,可取$\overrightarrow{n}$=(3,-$\sqrt{3}$,2),
∵平面DEH与y轴垂直,故其法向量可取为$\overrightarrow{j}$=(0,1,0),
cos<$\overrightarrow{j}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{j}•\overrightarrow{n}}{丨\overrightarrow{j}丨丨\overrightarrow{n}丨}$=$\frac{-\sqrt{3}}{1×4}$=-$\frac{\sqrt{3}}{4}$,
∴平面BCHG与平面DEH所成二面角的正弦值$\sqrt{1-(-\frac{\sqrt{3}}{4})^{2}}$=$\frac{\sqrt{13}}{4}$.
点评 本题考查面面垂直的性质,线面垂直,考查面面角,考查法向量的运用,考查数形结合思想,属于中档题.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案| 损坏餐椅数 | 未损坏餐椅数 | 总 计 | |
| 学习雷锋精神前 | 50 | 150 | 200 |
| 学习雷锋精神后 | 30 | 170 | 200 |
| 总 计 | 80 | 320 | 400 |
(2)请说明是否有97.5%以上的把握认为损毁餐椅数量与学习雷锋精神有关?
| A. | {-1,0,1} | B. | {0,$\frac{4\sqrt{6}}{9}$} | C. | {0,$\frac{2\sqrt{3}}{3}$} | D. | {-$\frac{4\sqrt{6}}{9}$,0,$\frac{4\sqrt{6}}{9}$} |
| 学生的编号i | 1 | 2 | 3 | 4 | 5 |
| 数学xi | 80 | 75 | 70 | 65 | 60 |
| 物理yi | 70 | 66 | 68 | 64 | 62 |
(Ⅱ)通过大量事实证明发现,一个学生的数学成绩和物理成绩具有很强的线性相关关系的,在上述表格是正确的前提下,用x表示数学成绩,用y表示物理成绩,求y与x的回归方程;
参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x.