题目内容
16.在等差数列{an}中,已知a3=2,a6+a10=20,则数列{an}的前10项和S10的值为( )| A. | 120 | B. | 100 | C. | 66 | D. | 60 |
分析 依题意,求出a8=10,再利用等差数列前n项和公式能求出数列{an}的前10项和S10的值.
解答 解:∵在等差数列{an}中,a3=2,a6+a10=20,
∴依题意,有a6+a10=2a8,∴a8=10,
∴${S_{10}}=\frac{{10({a_1}+{a_{10}})}}{2}=5({a_3}+{a_8})=60$.
故选:D.
点评 本题考查等差数列的前10项和的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
相关题目
7.某班50名学生右眼视力的检查结果如表所示:
则该班学生右眼视力的众数为1.2,中位数为0.8.
| 视力 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 1.0 | 1.2 | 1.5 |
| 人数 | 1 | 1 | 3 | 4 | 3 | 4 | 4 | 6 | 8 | 10 | 6 |
5.计算 (1+i)(1-i)=( )
| A. | 2i | B. | 1-2i | C. | 2 | D. | 0 |
 如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2$\sqrt{2}$,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2$\sqrt{2}$,∠BAC=90°,O为BC中点.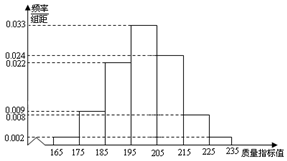 从某企业的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:求这500件产品质量指标值的样本平均数$\overline{x}$和样本方差s2(同一组数据用该区间的中点值作代表).
从某企业的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:求这500件产品质量指标值的样本平均数$\overline{x}$和样本方差s2(同一组数据用该区间的中点值作代表).