题目内容
11.在等差数列{an}中,已知d=$\frac{1}{2}$,a1=-3,Sn=$\frac{15}{2}$,则an=4.分析 在等差数列{an}中,利用前n项和公式求出n,由此能求出an的值.
解答 解:在等差数列{an}中,
∵d=$\frac{1}{2}$,a1=-3,Sn=$\frac{15}{2}$,
∴${S}_{n}=-3n+\frac{n(n-1)}{2}×\frac{1}{2}$=$\frac{{n}^{2}-13n}{4}$=$\frac{15}{2}$,
解得n=15或n=-2(舍),
∴an=a15=a1+14d=-3+14×$\frac{1}{2}$=4.
故答案为:4.
点评 本题考查等差数列的第n基项的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
2.函数y=tanx(-$\frac{π}{4}$≤x≤$\frac{π}{4}$且x≠0)的值域是( )
| A. | [-1,1] | B. | [-1,0)∪(0,1] | C. | (-∞,1] | D. | [-1,+∞) |
19.在第二届乌镇互联网大会中,为了提高安保的级别同时又为了方便接,现将其中的五个参会国的人员安排酒店住宿,这五个参会国要在a、b、c三家酒店选择一家,且每家酒店至少有一个参会国入住,则这样的安排方法共有( )
| A. | 96种 | B. | 124种 | C. | 130种 | D. | 150种 |
16.在等差数列{an}中,已知a3=2,a6+a10=20,则数列{an}的前10项和S10的值为( )
| A. | 120 | B. | 100 | C. | 66 | D. | 60 |
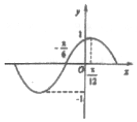 函数f(x)=sin(ωx+φ)(ω<0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将y=f(x)的图象向右平移$\frac{π}{4}$个单位长度后得到函数y=g(x)的图象.
函数f(x)=sin(ωx+φ)(ω<0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将y=f(x)的图象向右平移$\frac{π}{4}$个单位长度后得到函数y=g(x)的图象.