题目内容

已知
OA
=（0，-1），
OB
=（2，3），
OC
=（2，-1）
（Ⅰ）求
AB
•
AC
；
（Ⅱ）若
AC
•（
a
+
AC
）=6，
a
与
AC
的夹角为
π
3
，求|
a
-
AC
|的值．
考点：平面向量数量积的运算,数量积表示两个向量的夹角
专题：计算题,平面向量及应用
分析：（Ⅰ）先求出
AB
、
AC
，再利用向量的数量积公式求
AB
•
AC
；
（Ⅱ）先求出|
a
|=2，再求|
a
-
AC
|的值．
解答： 解：（Ⅰ）∵
OA
=（0，-1），
OB
=（2，3），
OC
=（2，-1）
∴
AB
=（2，4），
AC
=（2，0），
∴
AB
•
AC
=4；
（Ⅱ）∵
AC
•（
a
+
AC
）=6，
a
与
AC
的夹角为
π
3
，
∴2|
a
|cos
π
3
+4=6，
∴|
a
|=2，
∴|
a
-
AC
|=
4+4-2•2•2•
1
2
=2．
点评：本题考查向量的数量积公式，考查学生的计算能力，正确运用公式是关键．
练习册系列答案
相关题目
已知函数f（x）=
1
3
x3-
1
2
(2a+1)x2+(a2+a)x．若函数f（x）在x=1处取得极大值，则实数a的值为（　　）
A、1B、0C、2D、0或1
已知数列{an}中，a1=1，an+1=
an
an+3
（n∈N*）．
（1）求证：{
1
an
+
1
2
}为等比数列，并求{an}的通项公式an；
（2）数列{bn}满足bn=（3n-1）•
n
2n
•an，求数列{bn}的前n项和Tn．
已知函数f（x）=cosωx（sinωx-
3
cosωx），（ω＞0，x∈R）的最小正周期为π．
（Ⅰ）求实数ω的值．
（Ⅱ）在△ABC中，角A、B、C对应的边分别为a、b、c，若f（
B
2
）=
2
-
6
-2
3
4
，|
AB
+
AC
|=|
AB
-
AC
|=8，求△ABC的周长．
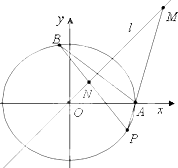已知A（2，0），B（x0，y0）是椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）上两点，满足直线AB的斜率为-
3
4
，且线段AB被直线l：y=x平分．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设点P是椭圆C上异于A，B的动点，若直线AP交M于点M，直线交l于点，试探究
OM
•
ON
是否为定值，并说明理由．
已知实数a≠0，函数f（x）=
2x+a ， x＜1
-x-2a， x≥1

（1）若a=-3，求f（10），f（f（10））的值；
（2）若f（1-a）=f（1+a），求a的值．
△ABC中，BC边上的高AD=BC，角A，B，C所对的边分别是a，b，c，则
b
c
+
c
b
的取值范围是
 
．
已知函数f（x）=ex-a（x+1）在x=ln2处的切线的斜率为1．（e为无理数，e=271828…）
（Ⅰ）求a的值及f（x）的最小值；
（Ⅱ）当x≥0时，f（x）≥mx2，求m的取值范围；
（Ⅲ）求证：
n
i=2
lni
i4
＜
1
2e
（i，n∈N+）．（参考数据：ln2≈0.6931）
已知直线l1：ax+2y+6=0，直线l2：x+（a-1）y+a2-1=0．当a
 
时，l1与l2相交；当a
 
时，l1⊥l2；当a
 
时，l1与l2重合；当a
 
时，l1∥l2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网