题目内容
17.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{4}$=1(a∈N*)的两个焦点为F1,F2,P为该双曲线上一点,满足|F1F2|2=|PF1|•|PF2|,P到坐标原点O的距离为d,且5<d<7,则a2=4.分析 求得双曲线的b,c,设P为右支上一点,|PF1|=m,|PF2|=n,运用双曲线的定义,结合条件,由两点的距离公式,解不等式可得a的正整数解.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{4}$=1的b=2,c2=a2+4,
设P为右支上一点,|PF1|=m,|PF2|=n,
由双曲线的定义可得m-n=2a,
由题意可得4c2=mn,
m2+n2=2c2+2d2,
可得(m-n)2+2mn=4a2+8c2=2c2+2d2
又d2∈(25,49),
即25<5a2+12<49,
由a为正整数,可得a=2,
故答案为:4.
点评 本题考查双曲线的定义、方程和性质,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
11.若向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2,($\overrightarrow{a}$+$\overrightarrow{b}$)$•\overrightarrow{b}$=6,则$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
2.设a=tan$\frac{π}{7}$,b=$\frac{π}{7}$,c=sin$\frac{π}{7}$,则a,b,c的大小关系是( )
| A. | c>b>a | B. | b>c>a | C. | a>c>b | D. | a>b>c |
9.将函数y=sinx的图象向右平移$\frac{π}{6}$个单位,再将所得函数图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=sin(ωx+φ),(ω>0,|φ|<$\frac{π}{2}$)的图象,则( )
| A. | ω=2,φ=-$\frac{π}{6}$ | B. | ω=2,φ=-$\frac{π}{3}$ | C. | ω=$\frac{1}{2}$,φ=-$\frac{π}{6}$ | D. | ω=$\frac{1}{2}$,φ=-$\frac{π}{3}$ |
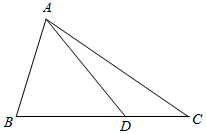 如图,在△ABC中,AB=2,cosB=$\frac{1}{3}$,点D在线段BC上.
如图,在△ABC中,AB=2,cosB=$\frac{1}{3}$,点D在线段BC上.