题目内容
5.设a为实数,函数f(x)=x3-x2-x+a,若函数f(x)过点A(1,0),求函数在区间[-1,3]上的最值.分析 由题意可得f(1)=1-1-1+a=0,从而化简f(x)=x3-x2-x+1,f′(x)=3x2-2x-1=(3x+1)(x-1),从而判断函数的单调性再求最值即可.
解答 解:∵函数f(x)过点A(1,0),
∴f(1)=1-1-1+a=0,
∴a=1,
∴f(x)=x3-x2-x+1,f′(x)=3x2-2x-1=(3x+1)(x-1),
∴f(x)在[-1,-$\frac{1}{3}$]上是增函数,在[-$\frac{1}{3}$,1]上是减函数,
在[1,3]上是增函数;
而f(-1)=-1-1+1+1=0,
f(-$\frac{1}{3}$)=-$\frac{1}{27}$-$\frac{1}{9}$+$\frac{1}{3}$+1=1+$\frac{5}{27}$=$\frac{32}{27}$,
f(1)=0,
f(3)=27-9-3+1=16,
故函数f(x)的最大值为16,最小值为0.
点评 本题考查了函数的性质的判断与应用,同时考查了导数的综合应用,属于中档题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
19.不等式y≥2x-3表示的平面区域是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
13.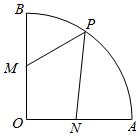 如图,扇形AOB中,OA=1,∠AOB=90°,M是OB中点,P是弧AB上的动点,N是线段OA上的动点,则$\overrightarrow{PM}$$•\overrightarrow{PN}$的最小值为( )
如图,扇形AOB中,OA=1,∠AOB=90°,M是OB中点,P是弧AB上的动点,N是线段OA上的动点,则$\overrightarrow{PM}$$•\overrightarrow{PN}$的最小值为( )
 如图,扇形AOB中,OA=1,∠AOB=90°,M是OB中点,P是弧AB上的动点,N是线段OA上的动点,则$\overrightarrow{PM}$$•\overrightarrow{PN}$的最小值为( )
如图,扇形AOB中,OA=1,∠AOB=90°,M是OB中点,P是弧AB上的动点,N是线段OA上的动点,则$\overrightarrow{PM}$$•\overrightarrow{PN}$的最小值为( )| A. | 0 | B. | 1 | C. | $\frac{3}{2}$ | D. | 1-$\frac{\sqrt{5}}{2}$ |
20.下列说法正确的是( )
| A. | 两两相交的三条直线共面 | |
| B. | 两条异面直线在同一平面上的射影可以是一条直线 | |
| C. | 一条直线上有两点到平面的距离相等,则这条直线和该平面平行 | |
| D. | 不共面的四点中,任何三点不共线. |
17.已知$\overrightarrow{a}$,$\overrightarrow{b}$是非零向量,则“|$\overrightarrow{a}$•$\overrightarrow{b}$|=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|”是“$\overrightarrow{a}$∥$\overrightarrow{b}$”成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分条件又不必要条件 |
14.方程C${\;}_{16}^{{x}^{2}-x}$=C${\;}_{16}^{5x-5}$的解集是( )
| A. | {1,3,5,7} | B. | {1,3,5} | C. | {3,5} | D. | {1,3} |
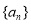 是公差为正数的等差数列,其前
是公差为正数的等差数列,其前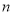 项和为
项和为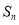 ,且
,且 ,
,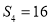 .
.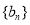 满足
满足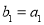 ,
,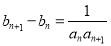 .
.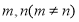 ,使得
,使得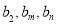 成等差数列?若存在,求出
成等差数列?若存在,求出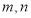 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.