题目内容
6.计算:${∫}_{-1}^{1}$f(x)dx,其中f(x)=$\left\{\begin{array}{l}{{x}^{2}+1,0≤x≤1}\\{x-1,-1≤x<0}\end{array}\right.$.分析 根据分段函数得到${∫}_{-1}^{1}$f(x)dx=${∫}_{-1}^{0}$(x-1)dx+${∫}_{0}^{1}$(x2+1)dx,计算即可.
解答 解:${∫}_{-1}^{1}$f(x)dx=${∫}_{-1}^{0}$(x-1)dx+${∫}_{0}^{1}$(x2+1)dx=($\frac{1}{2}{x}^{2}$-x)|${\;}_{-1}^{0}$+($\frac{1}{3}{x}^{3}$+x)|${\;}_{0}^{1}$=0-($\frac{1}{2}$+1)+$\frac{1}{3}$+1=-$\frac{1}{6}$
点评 本题考查了的定积分的计算以及分段函数,属于基础题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
17.已知$\overrightarrow{a}$,$\overrightarrow{b}$是非零向量,则“|$\overrightarrow{a}$•$\overrightarrow{b}$|=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|”是“$\overrightarrow{a}$∥$\overrightarrow{b}$”成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分条件又不必要条件 |
14.方程C${\;}_{16}^{{x}^{2}-x}$=C${\;}_{16}^{5x-5}$的解集是( )
| A. | {1,3,5,7} | B. | {1,3,5} | C. | {3,5} | D. | {1,3} |
11.已知复数z的共轭复数$\overline{z}$,且$\overline{z}=\frac{z}{1+i}$+2(i为虚数单位),则z在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
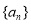 是公差为正数的等差数列,其前
是公差为正数的等差数列,其前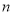 项和为
项和为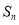 ,且
,且 ,
,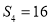 .
.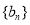 满足
满足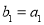 ,
,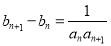 .
.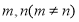 ,使得
,使得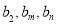 成等差数列?若存在,求出
成等差数列?若存在,求出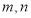 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 满足
满足 ,则
,则 的共轭复数的虚部是( )
的共轭复数的虚部是( ) B.
B. C.
C. D.
D.