题目内容
11.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(0,1),且圆x2+y2=a2被直线x-y-$\sqrt{2}$=0截得的弦长为2(1)求椭圆C的标准方程;
(2)已知k≠0,动直线y=k(x-1)与椭圆C的两个交点分别为A,B,问:在x轴上是否存在定点M,使得$\overrightarrow{MA}$$•\overrightarrow{MB}$为定值?若存在,试求出点M的坐标和定值;若不存在,请说明理由.
分析 (1)椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(0,1),代入解得b=1.由于圆x2+y2=a2被直线x-y-$\sqrt{2}$=0截得的弦长为2,可得2$\sqrt{{a}^{2}-(\frac{\sqrt{2}}{\sqrt{2}})^{2}}$=2,解得a2.即可得出.
(2)设A(x1,y1),B(x2,y2),M(m,0).直线方程与椭圆方程联立化为:(1+2k2)x2-4k2x+2k2-2=0,利用根与系数的关系代入$\overrightarrow{MA}$$•\overrightarrow{MB}$=(x1-m)(x2-m)+y1y2=m2+$\frac{{k}^{2}(1-4m)-2}{1+2{k}^{2}}$,令1-4m=-4,即可得出.
解答 解:(1)∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(0,1),∴$0+\frac{1}{{b}^{2}}$=1,解得b=1.
∵圆x2+y2=a2被直线x-y-$\sqrt{2}$=0截得的弦长为2,∴2$\sqrt{{a}^{2}-(\frac{\sqrt{2}}{\sqrt{2}})^{2}}$=2,解得a2=2.
∴椭圆C的标准方程为$\frac{{x}^{2}}{2}+{y}^{2}$=1.
(2)设A(x1,y1),B(x2,y2),M(m,0).
联立$\left\{\begin{array}{l}{y=k(x-1)}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,化为:(1+2k2)x2-4k2x+2k2-2=0,
∴x1+x2=$\frac{4{k}^{2}}{1+2{k}^{2}}$,x1x2=$\frac{2{k}^{2}-2}{1+2{k}^{2}}$.
∴$\overrightarrow{MA}$$•\overrightarrow{MB}$=(x1-m)(x2-m)+y1y2
=(k2+1)x1x2-(m+k2)(x1+x2)+m2+k2
=$\frac{({k}^{2}+1)(2{k}^{2}-2)}{1+2{k}^{2}}$-$\frac{(m+{k}^{2})×4{k}^{2}}{1+2{k}^{2}}$+m2+k2=m2+$\frac{{k}^{2}(1-4m)-2}{1+2{k}^{2}}$,
令1-4m=-4,即m=$\frac{5}{4}$时,$\overrightarrow{MA}$$•\overrightarrow{MB}$=m2-2=-$\frac{7}{16}$为定值.
点M$(\frac{5}{4},0)$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、一元二次方程的根与系数的关系、向量数量积运算性质,考查了推理能力与计算能力,属于难题.

| A. |  | B. |  | ||
| C. |  | D. |  |

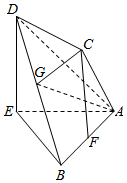 如图,异面直线AB,CD互相垂直,CF是它们的公垂线段,且F为AB的中点,作DE$\stackrel{∥}{=}$CF,连接AC、BD,G为BD的中点,AB=AC=AE=BE=2.
如图,异面直线AB,CD互相垂直,CF是它们的公垂线段,且F为AB的中点,作DE$\stackrel{∥}{=}$CF,连接AC、BD,G为BD的中点,AB=AC=AE=BE=2.