题目内容
| a |
| b |
| a |
| b |
| a |
| b |
| A、锐角 | B、直角 | C、钝角 | D、π |
考点：平面向量数量积的坐标表示、模、夹角
专题：平面向量及应用
分析：首先，写出
+
=(5，5)，
-
=(-1，-3)，然后，求解向量的夹角．
| a |
| b |
| a |
| b |
解答：
解：∵
=（2，1），
=（3，4），则
+
=(5，5)，
-
=(-1，-3)，
∴|
+
|=
=5
，
|
-
|=
=5，
设向量
+
与
-
的夹角为θ，
∴cosθ=
=
=-
＜0，
∴θ为钝角，
故选：C．
| a |
| b |
| a |
| b |
| a |
| b |
∴|
| a |
| b |
| 52+52 |
| 2 |
|
| a |
| b |
| 32+42 |
设向量
| a |
| b |
| a |
| b |
∴cosθ=
(
| ||||||||
|
|
| -20 | ||
25
|
2
| ||
| 5 |
∴θ为钝角，
故选：C．
点评：本题重点考查了向量的坐标运算，向量的夹角公式及其应用，属于中档题．
练习册系列答案
相关题目
由函数y=cosx与x=0，x=
π，y=0围成的几何图形的面积为（ ）
| 5 |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
某几何体的三视图如图所示，则该几何体的体积为（ ）
A、
| ||||
B、5+
| ||||
C、5+
| ||||
D、
|
若函数f（x）为偶函数，x＞0时，f（x）单调递增，P=f（-π），Q=f（e），R=f（
），则P，Q，R的大小为（ ）
| 2 |
| A、R＞Q＞P |
| B、P＞Q＞R |
| C、P＞R＞Q |
| D、Q＞R＞P |
已知tan2α=
，α∈（0，
），则
=（ ）
| 3 |
| 4 |
| π |
| 4 |
| sinα+cosα |
| sinα-cosα |
| A、1 | B、-1 | C、2 | D、-2 |
已知i为虚数单位，a为实数，复数z=（a-2i）•i在复平面内对应的点为M，则“a=-1”是“点M在第四象限”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知向量
=（-1，1），
=（3，m），若
⊥
，则实数m=（ ）
| a |
| b |
| a |
| b |
| A、1 | B、-1 | C、3 | D、-3 |
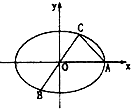如图，已知椭圆