题目内容
已知△ABC的内角A的大小为120°,面积为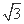
.
(1) 若AB=2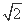
,求△ABC的另外两条边长;
(2) 设O为△ABC的外心,当BC=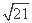
时,求
·
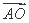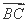的值.
(1) 设△ABC的内角A,B,C的对边分别为a,b,c,
于是=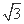
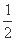bcsin A=
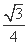bc,所以bc=4.
因为c=AB=2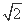,所以b=AC=.
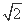由余弦定理得BC=a=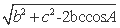
=
=
=
.
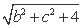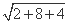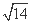(2) 由BC=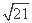,得b2+c2+4=21,
即b2+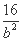
-17=0,解得b=1或4.
设BC的中点为D,则=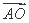
+
,
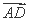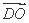因为O为△ABC的外心,所以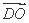·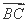=0,
于是·=·=(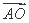
+
)·(-)=
.
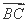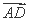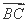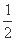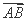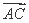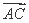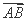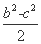所以当b=1时,c=4,·==-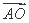
;
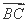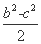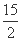当b=4时,c=1,·==.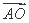
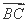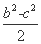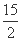练习册系列答案
口算题天天练系列答案
相关题目
上的一点,弦FA,FB分别与CD交于点G,H.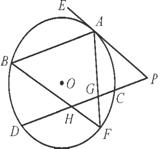
-
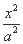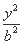=1(a>0,b>0)的右焦点,过F作双曲线C的一条渐近线的垂线,垂足为A,延长FA与另一条渐近线交于点B.若
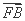=2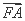
,则双曲线的离心率为 . 
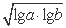,Q=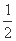
(lga+lgb),R=lg
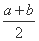,求P,Q,R的大小关系.
=
+
)·
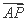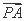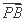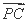的最小值是 . 
=
,则sin
+sin2
= . 
.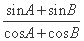