题目内容
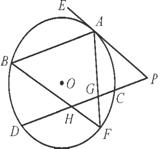
如图,已知AB,CD是圆O的两条平行弦,过点A引圆O的切线EP与DC的延长线交于点P,F为 上的一点,弦FA,FB分别与CD交于点G,H.
上的一点,弦FA,FB分别与CD交于点G,H.
(1) 求证:GP·GH=GC·GD;
(2) 若AB=AF=3GH=9,DH=6,求PA的长.
(1) 因为PE与圆O切于点A,
所以∠EAB=∠BFA.
因为AB∥CD,
所以∠EAB=∠APD.
在HGF和AGP中,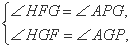
所以HGF∽△AGP,
所以GH·GP=GF·GA.
又因为GC·GD=GF·GA,
所以GP·GH=GC·GD.
(2) 因为AB=AF,
所以∠ABF=∠AFB=∠APH.
又因为AB∥CD,
所以四边形ABHP是平行四边形,
所以AB=PH=9,
所以GP=PH-GH=6,
所以GC=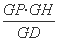 =
= =2,
=2,
所以PC=GP-GC=4.
因为PA是☉O的切线,
所以PA2=PC·PD,所以PA=2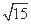 .
.

练习册系列答案
相关题目
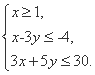
 的展开式的前三项的系数,求
的展开式的前三项的系数,求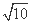 ,求圆O的半径OC的长.
,求圆O的半径OC的长.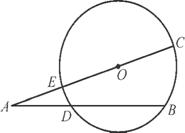
 BD,AN=
BD,AN=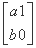 ,点A(1,0)在矩阵M对应变换作用下变为A'(1,2),求矩阵M的逆矩阵M-1.
,点A(1,0)在矩阵M对应变换作用下变为A'(1,2),求矩阵M的逆矩阵M-1.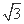 .
.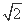 ,求△ABC的另外两条边长;
,求△ABC的另外两条边长;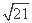 时,求
时,求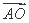 ·
·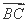 的值.
的值.