题目内容
13.已知抛物线C:y2=2px(p>0),过点A(12,0)作直线MN垂直x轴交抛物线于M、N两点,ME⊥ON于E,AE∥OM,O为坐标原点.(Ⅰ)求p的值;
(Ⅱ)若抛物线C上存在不同的两点G、H关于直线y=x+m对称,求m取值的范围.
分析 (Ⅰ)求出$M({12,4\sqrt{3}})$,代入y2=2px,求p的值;
(Ⅱ)设两对称点为G(x1,y1),H(x2,y2),由条件可设GH的方程为y=-x+b,与抛物线y2=4x消去y得关于x的一元二次方程,则△>0①,由韦达定理可表示GH中点横坐标,代入y=-x+b得其纵坐标,再代入y=x+m得m与b的方程,联立①即可求得m的取值范围,
解答 解:(Ⅰ)因为MN垂直x轴,所以M、N关于x轴对称,所以|OM|=|ON|.(1分)
又因为A是MN中点,AE∥OM,所以E是ON中点,(3分)
又ME⊥ON,所以|OM|=|MN|,所以△OMN是等边三角形,所以∠MOA=30°,(5分)
所以$M({12,4\sqrt{3}})$,代入y2=2px,得p=2.(6分)
(Ⅱ)因为GH与直线y=x+m垂直,所以可设GH的方程为y=-x+b,(7分)
由$\left\{\begin{array}{l}y=-x+b\\{y^2}=4x\end{array}\right.$,得y2+4y-4b=0,(8分)
由△=16+16b>0得b>-1,(9分)
设G(x1,y1),H(x2,y2),GH的中点为P(x0,y0),
由y1+y2=-4,得${y_0}=\frac{{{y_1}+{y_2}}}{2}=-2$,
代入y=-x+b得x0=b+2,(10分)
又因为P(x0,y0)在直线y=x+m上,所以有-2=b+2+m,得b=-4-m,(11分)
结合b>-1,得m取值的范围为(-∞,-3).(12分)
点评 本题考查直线与圆锥曲线的位置关系,考查轴对称问题,本题采用“方程、不等式”法,解决本题的关键是用数学式子充分刻画条件:两点关于直线对称.

练习册系列答案
相关题目
4.下列式子中表示正确的是( )
| A. | 2+cosx=4 | B. | $\sqrt{10}$>π | C. | sinx•cosx=sin2x | D. | sin75°>cos14° |
1.已知顶点为原点,对称轴为坐标轴的抛物线的焦点在直线x-2y-2=0上,则此抛物线的标准方程是( )
| A. | y2=8x | B. | x2=4y | C. | y2=8x或x2=-4y | D. | y2=8x或x2=4y |
18.设fn(x)是等比数列1,x,x2,…,xn的各项和,则fn(2)等于( )
| A. | 2n-1 | B. | 2n+1-1 | C. | 2n-2 | D. | 2n+1-2 |
3.设全集U={1,2,3,4,5},A={1,5},B={2,4},则B∩(∁UA)=( )
| A. | {2,3,4} | B. | {2} | C. | {2,4} | D. | {1,3,4,5} |
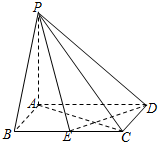 如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,点E为BC的中点.
如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,点E为BC的中点.