题目内容
10.已知函数f(x)=|log2|x||-($\frac{1}{2}$)x,则下列结论正确的是( )| A. | f(x)有三个零点,且所有零点之积大于-1 | |
| B. | f(x)有三个零点,且所有零点之积小于-1 | |
| C. | f(x)有四个零点,且所有零点之积大于1 | |
| D. | f(x)有四个零点,且所有零点之积小于1 |
分析 函数f(x)是一个对数函数减去一个指数函数.由绝对值的性质知,
解答 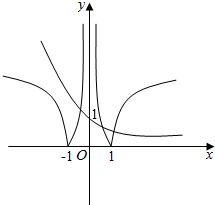 解:对数函数y=|log2|x||的图象是对数函数y=log2x的图象将x轴下侧图象翻到x轴上方之后再关于y轴对称得到.
解:对数函数y=|log2|x||的图象是对数函数y=log2x的图象将x轴下侧图象翻到x轴上方之后再关于y轴对称得到.
其函数图象与指数函数y=${(\frac{1}{2})}^{x}$的图象有3个交点,所以函数f(x)有3个零点.
∵|${log}_{2}\frac{1}{\sqrt{2}}$|=$\frac{1}{2}$,${log}_{2}\sqrt{2}$=$\frac{1}{2}$
而${(\frac{1}{2})}^{1}$=$\frac{1}{2}$,
∴对数函数y=|log2|x||与指数函数y=${(\frac{1}{2})}^{x}$的两个交点分别在(0,$\frac{1}{\sqrt{2}}$)与(1,$\sqrt{2}$)之间,
这两个交点的乘积小于$\frac{1}{\sqrt{2}}×\sqrt{2}$=1
而第三个交点在(-$\frac{1}{2}$,0)之间,
∴三个交点的积小于-1.
即函数f(x)的3个零点的积小于-1
故选:B.
点评 本题考查的是将一个复杂函数求零点问题转化为对数函数与指数函数图象相交的交点问题.而且对函数绝对值问题也需熟练掌握.

练习册系列答案
相关题目
20.已知x与y之间的一组数据:
则y与x的线性回归方程为$\hat y=bx+a$必过点(2.5,2).
| x | 1 | 2 | 3 | 4 |
| y | 1 | 3 | 5 | 7 |
1.已知顶点为原点,对称轴为坐标轴的抛物线的焦点在直线x-2y-2=0上,则此抛物线的标准方程是( )
| A. | y2=8x | B. | x2=4y | C. | y2=8x或x2=-4y | D. | y2=8x或x2=4y |
18.设fn(x)是等比数列1,x,x2,…,xn的各项和,则fn(2)等于( )
| A. | 2n-1 | B. | 2n+1-1 | C. | 2n-2 | D. | 2n+1-2 |