��Ŀ����
16����֪�Ȳ�����{an}Ϊ�������У���a1=1��{bn}Ϊ�ȱ����У���a2=b2��a5=b3��a14=b4����1����{an}��{bn}��ͨ�ʽ��
��2����֪����{cn}���㣺an+1=$\frac{{c}_{1}}{{b}_{1}}$+$\frac{{c}_{2}}{{b}_{2}}$+��+$\frac{{c}_{n}}{{b}_{n}}$��������{an•cn}��ǰn���Sn��
���� ��1��������Ȳ�����{an}�Ĺ���Ϊd��0����a1=1���ȱ�����{bn}�Ĺ���Ϊq����a2=b2��a5=b3��a14=b4���ɵ�1+d=b1q��1+4d=${b}_{1}{q}^{2}$��1+13d=${b}_{1}{q}^{3}$������������ɵó���
��2��cn=2��3n-1���ɵ�an•cn=��4n-2��•3n-1�������á���λ���������ȱ����е�ǰn���ʽ���ɵó���
��� �⣺��1��������Ȳ�����{an}�Ĺ���Ϊd��0����a1=1���ȱ�����{bn}�Ĺ���Ϊq����a2=b2��a5=b3��a14=b4��
��1+d=b1q��1+4d=${b}_{1}{q}^{2}$��1+13d=${b}_{1}{q}^{3}$��
�������d=2��q=3��b1=1��
��an=1+2��n-1��=2n-1��
bn=3n-1��
��2����an+1=$\frac{{c}_{1}}{{b}_{1}}$+$\frac{{c}_{2}}{{b}_{2}}$+��+$\frac{{c}_{n}}{{b}_{n}}$��
�൱n=1ʱ��a2=$\frac{{c}_{1}}{{b}_{1}}$�����c1=3��
��n��2ʱ��an=$\frac{{c}_{1}}{{b}_{1}}$+$\frac{{c}_{2}}{{b}_{2}}$+��+$\frac{{c}_{n-1}}{{b}_{n-1}}$���ɵ�an+1-an=$\frac{{c}_{n}}{{b}_{n}}$=2��
��cn=2��3n-1��
��an•cn=��4n-2��•3n-1��
������{an•cn}��ǰn���Sn=2+6��3+��+��4n-2��•3n-1��
3Sn=2��3+6��32+��+��4n-6��•3n-1+��4n-2��•3n��
��-2Sn=2+4��3+32+��+3n-1��-��4n-2��•3n=2+4��$\frac{3��{3}^{n-1}-1��}{3-1}$-��4n-2��•3n=��4-4n��•3n-4��
���Sn=2+��2n-2��•3n��
���� ���⿼���˵��ƹ�ϵ��Ӧ�á���������˼�뷽����������ͷ������ȱ����е�ͨ�ʽ��������������������������������е��⣮

 ȫ�ų��100��ϵ�д�
ȫ�ų��100��ϵ�д� Ӣ�ŵ��ϵ�д�
Ӣ�ŵ��ϵ�д�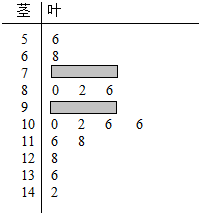 ij��ѧ��ʦ�Ա�У2013�����ѧ���ĸ߿���ѧ�ɼ���1��200���зֲ������ȡ��20��ѧ���ijɼ������þ�Ҷͼ��¼������ͼ��ʾ�����������ݲ�С�Ķ�ʧ��ͬʱ�õ�������ʾ��Ƶ�ʷֲ�����
ij��ѧ��ʦ�Ա�У2013�����ѧ���ĸ߿���ѧ�ɼ���1��200���зֲ������ȡ��20��ѧ���ijɼ������þ�Ҷͼ��¼������ͼ��ʾ�����������ݲ�С�Ķ�ʧ��ͬʱ�õ�������ʾ��Ƶ�ʷֲ�����| �����Σ��֣� | [50��70�� | [70��90�� | [90��110�� | [110��130�� | [130��150�� | �ܼ� |
| Ƶ�� | b | |||||
| Ƶ�� | a | 0.25 |
��2���������[90��100����Χ�ڵ�ѧ����������������ο���ȫУѧ����ѧ�ɼ��ļ����ʣ�������[90��150����Ϊ����
��3���ӳɼ���[100��130����Χ�ڵ�ѧ�������ѡ4�ˣ������гɼ���[100��110���ڵ��������2�˵ĸ��ʣ�
| A�� | 2+cosx=4 | B�� | $\sqrt{10}$���� | C�� | sinx•cosx=sin2x | D�� | sin75�㣾cos14�� |
| A�� | y2=8x | B�� | x2=4y | C�� | y2=8x��x2=-4y | D�� | y2=8x��x2=4y |
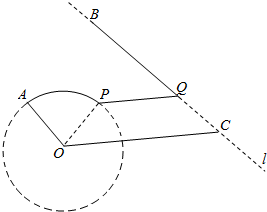 ��ͼ��B��C�Ǻ�����l�����50km����������С�ǣ�ԲO�ǰ뾶Ϊ10km��ij����С�ǵĻ���·��AΪԲO�ϵ�������תվ�����С�AOC=$\frac{2}{3}$�У�OC=25km����l��OA��Ϊʹ��תվA����������B�ǣ��ƻ���A���ػ���·��ij��P������ˮ·PQ��������l��Q������غ�����QB��B���������ߣ�����PQ��OC��Q���߶�BC�ϣ�
��ͼ��B��C�Ǻ�����l�����50km����������С�ǣ�ԲO�ǰ뾶Ϊ10km��ij����С�ǵĻ���·��AΪԲO�ϵ�������תվ�����С�AOC=$\frac{2}{3}$�У�OC=25km����l��OA��Ϊʹ��תվA����������B�ǣ��ƻ���A���ػ���·��ij��P������ˮ·PQ��������l��Q������غ�����QB��B���������ߣ�����PQ��OC��Q���߶�BC�ϣ�