题目内容
11.f(x)是奇函数,对任意的实数x,y,有f(x+y)=f(x)+f(y),且当x<0时,f(x)>0,则f(x)在区间[a,b]上( )| A. | 有最小值f(a) | B. | 有最大值f(a) | C. | 有最大值$f(\frac{a+b}{2})$ | D. | 有最小值$f(\frac{a+b}{2})$ |
分析 根据函数奇偶性和单调性的定义和性质判断函数的单调性即可.
解答 解:设x1<x2,则设x1-x2<0,此时f(x1-x2)>0,
∵f(x)是奇函数,
则即f(x1-x2)=f(x1)+f(-x2)>0,
即f(x1)-f(x2)>0,则f(x2)<f(x1),
即f(x)单调递减;
则函数f(x)在区间[a,b]上为减函数,则最大值为f(a),
故选:B.
点评 本题主要考查抽象函数的应用,利用赋值法结合函数单调性和奇偶性的定义是解决本题的关键.

练习册系列答案
相关题目
1.抛物线y=x2的准线方程是( )
| A. | $y=-\frac{1}{4}$ | B. | $y=-\frac{1}{2}$ | C. | $x=-\frac{1}{4}$ | D. | $x=-\frac{1}{2}$ |
2.关于命题p:A∩∅=∅,命题q:A∪∅=A,则下列说法正确的是( )
| A. | (¬p)∨q为假 | B. | (¬p)∧(¬q)为真 | C. | (¬p)∨(¬q)为假 | D. | (¬p)∧q为真 |
19.已知α∈(0,π)且$cos({\frac{π}{4}+α})=\frac{3}{5}$,则cosα的值为( )
| A. | $\frac{{\sqrt{2}}}{10}$ | B. | $-\frac{{\sqrt{2}}}{10}$ | C. | $\frac{{7\sqrt{2}}}{10}$ | D. | $-\frac{{7\sqrt{2}}}{10}$ |
20.已知x与y之间的一组数据:
则y与x的线性回归方程为$\hat y=bx+a$必过点(2.5,2).
| x | 1 | 2 | 3 | 4 |
| y | 1 | 3 | 5 | 7 |
1.已知顶点为原点,对称轴为坐标轴的抛物线的焦点在直线x-2y-2=0上,则此抛物线的标准方程是( )
| A. | y2=8x | B. | x2=4y | C. | y2=8x或x2=-4y | D. | y2=8x或x2=4y |
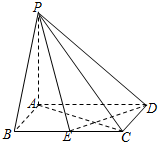 如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,点E为BC的中点.
如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,点E为BC的中点.