题目内容
点P是圆C:(x-3)2+(y+4)2=4上的动点,点O为坐标原点,则|OP|的最大值为( )
| A、5 | B、6 | C、7 | D、8 |
考点:圆方程的综合应用
专题:计算题,直线与圆
分析:求出圆心与半径,即可求出|OP|的最大值.
解答:
解:圆C:(x-3)2+(y+4)2=4的圆心坐标为C(3,-4),半径为r=2,则
∵点O为坐标原点,
∴|OP|的最大值为|OC|+r=5+2=7.
故选:C.
∵点O为坐标原点,
∴|OP|的最大值为|OC|+r=5+2=7.
故选:C.
点评:本题考查圆的方程,考查|OP|的最大值,正确利用圆的图形的特殊性是关键.

练习册系列答案
相关题目
某四面体的三视图均为直角三角形,如图,则该四面体的表面积为( )

A、72+24
| ||
B、96+24
| ||
| C、126 | ||
| D、64 |
已知函数f(x)=log3x,则f(27)=( )
| A、3 | B、9 | C、27 | D、81 |
已知点(1,3)和(3,-4)在直线l:2x-3y+a=0的两侧,则a的取值范围是( )
| A、(-∞,-18]∪(7,+∞) |
| B、(-18,7) |
| C、{-18,7} |
| D、不确定 |
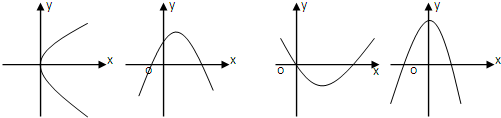
在下面的四个图象中,其中一个图象是函f(x)=
x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)的图象,则f(-1)等于( )
| 1 |
| 3 |

A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|