题目内容
将函数f(x)=sinx•cosx的图象向左平移φ个单位(φ>0),得到函数y=g(x)的图象,若y=g(x)的图象关于原点对称,则φ的值不可能是( )
A、
| ||
B、
| ||
| C、π | ||
| D、2π |
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:根据y=Asin(ωx+φ)的图象变换规律可得g(x)=
sin(2x+2φ),由y=g(x)的图象关于原点对称,可得2φ=kπ,k∈z,由此可得 φ 的值,结合所给的选项,得出结论.
| 1 |
| 2 |
解答:
解:将函数f(x)=sinx•cosx=
sin2x的图象向左平移φ个单位(φ>0),
得到函数y=g(x)=
sin2(x+φ)=
sin(2x+2φ)的图象,
由y=g(x)的图象关于原点对称,可得2φ=kπ,k∈z,即 φ=
.
故φ的值不可能是
,
故选:A.
| 1 |
| 2 |
得到函数y=g(x)=
| 1 |
| 2 |
| 1 |
| 2 |
由y=g(x)的图象关于原点对称,可得2φ=kπ,k∈z,即 φ=
| kπ |
| 2 |
故φ的值不可能是
| π |
| 4 |
故选:A.
点评:本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
某程序框图如图所示,该程序运行后输出的S为( )


A、-
| ||
| B、2 | ||
| C、-3 | ||
D、
|
点P是圆C:(x-3)2+(y+4)2=4上的动点,点O为坐标原点,则|OP|的最大值为( )
| A、5 | B、6 | C、7 | D、8 |
∫
|sinx|dx等于( )
|
| A、0 | B、1 | C、2 | D、4 |
已知变量x,y具有线性相关关系,测得(x,y)的一组数据如下:(0,1),(1,2),(2,4),(3,5),其回归方程为
=1.4x+a,则a的值等于( )
 |
| y |
| A、0.9 | B、0.8 |
| C、0.6 | D、0.2 |
某种饮料每箱装5听,其中有3听合格,2听不合格,现质检人员从中随机抽取2听进行检测,则检测出至少有一听不合格饮料的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
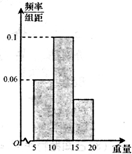 如图是一容量为100的样本的重量的频率分布直方图,样本重量均在[5,20]内,其分组为[5,10),[10,15),[15,20],则样本重量落在[15,20]内的频数为
如图是一容量为100的样本的重量的频率分布直方图,样本重量均在[5,20]内,其分组为[5,10),[10,15),[15,20],则样本重量落在[15,20]内的频数为