题目内容
18．已知tanα=$\frac{1}{3}$，则$\frac{1+cos2α}{sin2α}$=（ ）| A． | -$\frac{1}{3}$ | B． | $\frac{1}{3}$ | C． | -3 | D． | 3 |
分析 由条件利用同角三角函数的基本关系，二倍角公式，求得所给式子的值．
解答 解：∵tanα=$\frac{1}{3}$，则$\frac{1+cos2α}{sin2α}$=$\frac{{2cos}^{2}α}{2sinα•cosα}$=$\frac{cosα}{sinα}$=$\frac{1}{tanα}$=3，
故选：D．
点评 本题主要考查同角三角函数的基本关系，二倍角公式的应用，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
6．a，b满足2a+b=2，则直线ax+2y+b=0必过定点（ ）
| A． | （0，2-2a） | B． | （1，2） | C． | （2，2） | D． | （2，-1） |
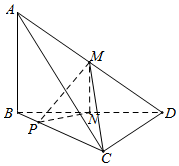在三棱锥A-BCD中，AB⊥平面BCD，DB=DC=4，∠BDC=90°，P在线段BC上，CP=3PB，M，N分别为AD，BD的中点．
3．函数f（x）=x2-x-1的零点有（ ）
| A． | 2个 | B． | 1个 | C． | 0个 | D． | 都有可能 |
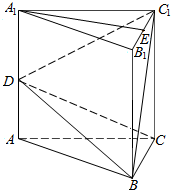三棱柱ABC-A1B1C1中，AA1⊥面ABC，BC⊥AC，AC=BC=1，AA1=2，点D、E分别为AA1、B1C1的中点．
8．经过点A（5，2），B（3，2），圆心在直线2x-y-3=0上的圆的方程为（ ）
| A． | （x-4）2+（y-5）2=10 | B． | （x+4）2+（y-5）2=10 | C． | （x-4）2+（y+5）2=10 | D． | （x+4）2+（y+5）2=10 |