题目内容
10.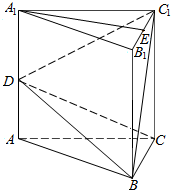 三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,AC=BC=1,AA1=2,点D、E分别为AA1、B1C1的中点.
三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,AC=BC=1,AA1=2,点D、E分别为AA1、B1C1的中点.(1)求三棱锥C1-DBC的体积${V_{{C_1}-DBC}}$
(2)求证:A1E∥面BC1D
(3)求证:面BC1D⊥面BCD.
分析 (1)证明BC⊥面AC1,利用${V_{{C_1}-DBC}}$=${V_{B-DC{C_1}}}$,求出三棱锥C1-DBC的体积${V_{{C_1}-DBC}}$
(2)求设C为坐标原点,建立如图所示的空间直角坐标系C-xyz,求出平面BC1D的一个法向量,证明$\overrightarrow{{A}_{1}E}$•$\overrightarrow{n}$=0,即可证明A1E∥面BC1D;
(3)求出平面BCD的一个法向量,证明$\overrightarrow{m}$•$\overrightarrow{n}$=0,即可证明面BC1D⊥面BCD.
解答 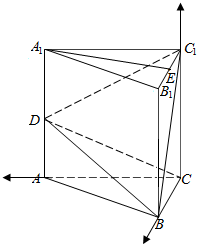 (1)解:∵AA1⊥面ABC,∴AA1⊥BC,
(1)解:∵AA1⊥面ABC,∴AA1⊥BC,
又BC⊥AC,且AA1∩AC=A,∴BC⊥面AC1
∴BC是三棱锥B-DCC1的高.
${V_{{C_1}-DBC}}$=${V_{B-DC{C_1}}}$=$\frac{1}{3}•(\frac{1}{2}•C{C_1}•AC)•BC$=$\frac{1}{3}$;(4分)
(2)证明:设C为坐标原点,建立如图所示的空间直角坐标系C-xyz
所以A(1,0,0),B(0,1,0),C(0,0,0),
A1(1,0,2),B1(0,1,2),C1(0,0,2).
因此E(0,$\frac{1}{2}$,0),D(1,0,1)
所以$\overrightarrow{{A}_{1}E}$=$(-1,\frac{1}{2},0)$
设平面BC1D的一个法向量$\overrightarrow{n}$=(x,y,z),
得:$\left\{\begin{array}{l}x-y+z=0\\-y+2z=0\end{array}\right.$∴$\left\{\begin{array}{l}x=1\\ y=2\\ z=1\end{array}\right.$
∴$\overrightarrow{n}$=(1,2,1)此时$\overrightarrow{{A}_{1}E}$•$\overrightarrow{n}$=-1+1=0.
∴A1E⊥$\overrightarrow{n}$,
∴A1E∥面BC1D(8分)
(3)证明:设平面BCD的一个法向量$\overrightarrow{m}$=(x,y,z),
得:$\left\{\begin{array}{l}x+z=0\\ y=0\end{array}\right.$∴$\overrightarrow{m}$=(1,0,-1)
此时$\overrightarrow{m}$•$\overrightarrow{n}$=(1,0,-1)•(1,2,1)=0
∴$\overrightarrow{m}$⊥$\overrightarrow{n}$,
∴面BC1D⊥面BCD(12分)
点评 本题考查几何体体积的计算,考查线面平行,平面与平面垂直的证明,考查向量法的运用,属于中档题.

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案| A. | ?x0∈R,f(x0)=0 | |
| B. | 若x0是f(x)的极小值点,则f(x)在区间(-∞,x0)上单调递减 | |
| C. | 函数f(x)的图象是中心对称图形 | |
| D. | 若x0是f(x)的极值点,则f′(x0)=0 |
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | -3 | D. | 3 |
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
| A. | 240 | B. | 300 | C. | 360 | D. | 400 |
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{3}{4}$ |