题目内容
8.在平面直角坐标系xoy中,已知曲线${C_1}:{x^2}+{y^2}=1$,以平面直角坐标系xoy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l:ρ(2cosθ-sinθ)=6.将曲线C1上的所有点的横坐标、纵坐标分别伸长为原来的$\sqrt{3}$、2倍后得到曲线C2,试写出直线l的直角坐标方程和曲线C2的参数方程.分析 根据极坐标与直角坐标的对应关系得出l的普通方程,根据图象变换先写出C2的普通方程,再转化为参数方程.
解答 解:∵ρ(2cosθ-sinθ)=6,即2ρcosθ-ρsinθ-6=0.
∴直线l的直角坐标方程为:2x-y-6=0,
曲线C2的直角坐标方程为:${(\frac{x}{{\sqrt{3}}})^2}+{(\frac{y}{2})^2}=1$,
令$\frac{x}{\sqrt{3}}$=cosθ,$\frac{y}{2}$=sinθ,则x=$\sqrt{3}$cosθ,y=2sinθ.
∴曲线C2的参数方程为:$\left\{\begin{array}{l}x=\sqrt{3}cosθ\\ y=2sinθ\end{array}\right.(θ为参数)$.
点评 本题考查了极坐标方程参数方程与普通方程的转化,属于基础题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
14.已知两个不共线的向量$\overrightarrow{OA}$和$\overrightarrow{OC}$,向量$\overrightarrow{OB}$与$\overrightarrow{OA}$关于向量$\overrightarrow{OC}$对称,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{b}$用$\overrightarrow{a}$和$\overrightarrow{c}$表示为( )
| A. | 2($\overrightarrow{a}$•$\overrightarrow{c}$)$\overrightarrow{c}$-$\overrightarrow{a}$ | B. | $\frac{2(\overrightarrow{a}•\overrightarrow{c})}{|\overrightarrow{c}|}•\overrightarrow{c}-\overrightarrow{a}$ | C. | $\frac{2(\overrightarrow{a}•\overrightarrow{c})}{|\overrightarrow{c}|}-\overrightarrow{a}$ | D. | $\frac{2(\overrightarrow{a}•\overrightarrow{c})}{|\overrightarrow{c}{|}^{2}}•\overrightarrow{c}-\overrightarrow{a}$ |
20.已知函数f(x)=x3+ax2+bx+c,下列结论中错误的是( )
| A. | ?x0∈R,f(x0)=0 | |
| B. | 若x0是f(x)的极小值点,则f(x)在区间(-∞,x0)上单调递减 | |
| C. | 函数f(x)的图象是中心对称图形 | |
| D. | 若x0是f(x)的极值点,则f′(x0)=0 |
17.若函数f(x)=4sin(ωx+φ)对任意的x都有f(${\frac{π}{3}$+x)=f(-x),则f($\frac{π}{6}}$)=( )
| A. | 0 | B. | -4或0 | C. | 4或0 | D. | -4或4 |
18.已知tanα=$\frac{1}{3}$,则$\frac{1+cos2α}{sin2α}$=( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | -3 | D. | 3 |
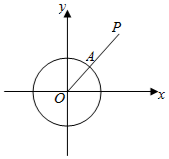 在平面直角坐标系xOy中,对于⊙O:x2+y2=1来说,P是坐标系内任意一点,点P到⊙O的距离SP的定义如下:若P与O重合,SP=r;若P不与O重合,射线OP与⊙O的交点为A,SP=AP的长度(如图).
在平面直角坐标系xOy中,对于⊙O:x2+y2=1来说,P是坐标系内任意一点,点P到⊙O的距离SP的定义如下:若P与O重合,SP=r;若P不与O重合,射线OP与⊙O的交点为A,SP=AP的长度(如图).