题目内容
8.经过点A(5,2),B(3,2),圆心在直线2x-y-3=0上的圆的方程为( )| A. | (x-4)2+(y-5)2=10 | B. | (x+4)2+(y-5)2=10 | C. | (x-4)2+(y+5)2=10 | D. | (x+4)2+(y+5)2=10 |
分析 由A和B的坐标求出直线AB的斜率,根据两直线垂直斜率的乘积为-1求出直线AB垂直平分线的斜率,根据垂径定理得到圆心在弦AB的垂直平分线上,又圆心在已知直线上,联立两直线方程组成方程组,求出方程组的解集,得到圆心M的坐标,再利用两点间的距离公式求出|AM|的长,即为圆的半径,由圆心坐标和半径写出圆的标准方程即可.
解答 解:∵A(5,2),B(3,2),
∴直线AB的斜率为0,
∴直线AB垂直平分线与x轴垂直,其方程为:x=4,
与直线2x-y-3=0联立解得:x=4,y=5,即所求圆的圆心M坐标为(4,5),
又所求圆的半径r=|AM|=$\sqrt{(5-4)^{2}+(2-5)^{2}}$=$\sqrt{10}$,
则所求圆的方程为(x-4)2+(y-5)2=10.
故选:A.
点评 此题考查了圆的标准方程,涉及的知识有:直线斜率的求法,两直线垂直时斜率满足的关系,两点间的距离公式,以及两直线的交点坐标求法,其中根据垂径定理得出弦AB的垂直平分线过圆心是解本题的关键.

练习册系列答案
相关题目
18.已知tanα=$\frac{1}{3}$,则$\frac{1+cos2α}{sin2α}$=( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | -3 | D. | 3 |
16.函数y=log3|x|的图象大致形状是( )
| A. | 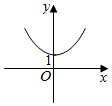 | B. |  | C. | 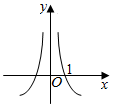 | D. | 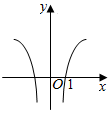 |
3.椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的短轴长为( )
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 4 | D. | 2 |
13.已知函数f(x)=3-ax+1的图象恒过定点P,则点P的坐标是( )
| A. | (0,3) | B. | (-1,2) | C. | (-1,3) | D. | (3,-1) |
20.过点M(2,-1)作斜率为$\frac{1}{2}$的直线与椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)相交于A,B两个不同点,若M是AB的中点,则该椭圆的离心率e=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{3}{4}$ |
17.下列命题成立的是( )
| A. | 如果a>b,c≠0,那么$\frac{a}{c}>\frac{b}{c}$ | B. | 如果a>b,那么a2>b2 | ||
| C. | 如果a>b,c>d,那么a+d>b+c | D. | 如果a>b,c>d,那么a-d>b-c |