题目内容
设x,y满足
求
(1)z=x2+y2的最大值和最小值
(2)z=
的最大值和最小值
(3)z=|2x-y+4|的最大值和最小值.
|
(1)z=x2+y2的最大值和最小值
(2)z=
| y |
| x-5 |
(3)z=|2x-y+4|的最大值和最小值.
考点:简单线性规划
专题:
分析:(1)作出不等式组对应的平面区域,利用x2+y2的几何意义求最小值.
(2)直线的斜率的最值求解即可.
(3)根据点到直线的距离公式,设d=
=
表示可行域内一点(x,y)到直线2x-y+4=0的距离的
倍.观察图形可得当可行域内点与B重合时,d达到最小值,由此即可算出z=|2x-y+4|最值.
(2)直线的斜率的最值求解即可.
(3)根据点到直线的距离公式,设d=
| |2x-y+4| | ||
|
| |2x-y+4| | ||
|
| 5 |
解答:
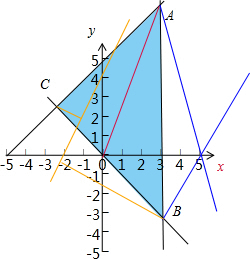 解:(1)设z=x2+y2,则z的几何意义为动点P(x,y)到原点距离的平方.
解:(1)设z=x2+y2,则z的几何意义为动点P(x,y)到原点距离的平方.
作出不等式组
对应的平面区域如图
由图象可知点A到原点的距离最大,
由
,可得A(3,8)
所以z=x2+y2的最大值为z=(3-0)2+(8-0)2=73.
x=0,y=0时,z=x2+y2的最小值为0.
(2)设P(x,y)为区域内的动点,可得
Z=
表示直线P、Q连线的斜率,其中Q(5,0)
运动点P,可得当P与A点重合时,Z=
=-4,取得最小值,k=-4,
当P与B点(3,-3)重合时,Z=
=
,达到最大值,
∴z=
的最大值和最小值分别为:
,-4.
(3)∵z=|2x-y+4|的几何意义是可行域内的点到直线2x-y+4=0的距离的
倍,
∴d=
,当可行域内的点在直线2x-y+4=0上时,距离最小,最小值为0,B到直线的距离最大,z=|2x-y+4|的最大值为:
×
=13.
 解:(1)设z=x2+y2,则z的几何意义为动点P(x,y)到原点距离的平方.
解:(1)设z=x2+y2,则z的几何意义为动点P(x,y)到原点距离的平方.作出不等式组
|
由图象可知点A到原点的距离最大,
由
|
所以z=x2+y2的最大值为z=(3-0)2+(8-0)2=73.
x=0,y=0时,z=x2+y2的最小值为0.
(2)设P(x,y)为区域内的动点,可得
Z=
| y |
| x-5 |
运动点P,可得当P与A点重合时,Z=
| 8-0 |
| 3-5 |
当P与B点(3,-3)重合时,Z=
| 0+3 |
| 5-3 |
| 3 |
| 2 |
∴z=
| y |
| x-5 |
| 3 |
| 2 |
(3)∵z=|2x-y+4|的几何意义是可行域内的点到直线2x-y+4=0的距离的
| 5 |
∴d=
| |2x-y+4| | ||
|
| 5 |
| |2×3-(-3)+4| | ||
|
点评:本题给出二元一次不等式组表示的平面区域,求几个目标函数的最值和取值范围.着重考查了平面内两点的距离公式、点到直线的距离公式和简单的线性规划等知识点,属于中档题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 如图所示的几何体是由一个棱长为2的正四面体和一个半圆锥组成,点O为半圆的圆心,E为BC的中点.
如图所示的几何体是由一个棱长为2的正四面体和一个半圆锥组成,点O为半圆的圆心,E为BC的中点.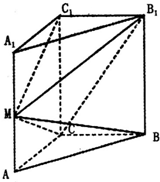 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,2AC=AA1=BC=2,M为AA1的中点.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,2AC=AA1=BC=2,M为AA1的中点.