题目内容
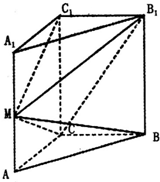 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,2AC=AA1=BC=2,M为AA1的中点.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,2AC=AA1=BC=2,M为AA1的中点.(1)求证直线C1M⊥平面BCM;
(2)求二面角C1-MC-B1的正切值.
考点:用空间向量求平面间的夹角,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)由题意知MC1=
,MC=
,C1C=2,由勾股定理得MC1⊥MC,从而BC⊥平面A1C,由此能证明MC1⊥平面BCM.
(2)由勾股定理得MB1⊥MC,又MC1⊥MC,从而∠B1MC1为所求二面角的平面角,由此能求出二面角C1-MC-B1的正切值.
| 2 |
| 2 |
(2)由勾股定理得MB1⊥MC,又MC1⊥MC,从而∠B1MC1为所求二面角的平面角,由此能求出二面角C1-MC-B1的正切值.
解答:
(1)证明:由题意知MC1=
,MC=
,C1C=2,
∴MC12+MC2=C1C2,∴MC1⊥MC,
∵BC⊥AC,BC⊥C1C,
∴BC⊥平面A1C,而MC1?平面{A1CA1C,
∴BC⊥MC1,又MC∩BC=C,
故MC1⊥平面BCM.
(2)解:∵MB1=
,MC=
,B1C=2
,
∴MB12+MC2=B1C2,即MB1⊥MC,
又MC1⊥MC,∴∠B1MC1为所求二面角的平面角,
在Rt△B1MC1中,tan∠B1MC1=
=
=
.
∴二面角C1-MC-B1的正切值为
.
| 2 |
| 2 |
∴MC12+MC2=C1C2,∴MC1⊥MC,
∵BC⊥AC,BC⊥C1C,
∴BC⊥平面A1C,而MC1?平面{A1CA1C,
∴BC⊥MC1,又MC∩BC=C,
故MC1⊥平面BCM.
(2)解:∵MB1=
| 2 |
| 6 |
| 2 |
∴MB12+MC2=B1C2,即MB1⊥MC,
又MC1⊥MC,∴∠B1MC1为所求二面角的平面角,
在Rt△B1MC1中,tan∠B1MC1=
| B1C1 |
| MC |
| 2 | ||
|
| 2 |
∴二面角C1-MC-B1的正切值为
| 2 |
点评:本题考查直线与平面垂直的证明,考查二面角的正切值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 一质点的移动方式,如图所示,在第1分钟,它从原点移动到点(1,0),接下来它便依图上所示的方向,在x,y轴的正向前进或后退,每1分钟只走1单位且平行其中一轴,则2013分钟结束之时,质点的位置坐标是
一质点的移动方式,如图所示,在第1分钟,它从原点移动到点(1,0),接下来它便依图上所示的方向,在x,y轴的正向前进或后退,每1分钟只走1单位且平行其中一轴,则2013分钟结束之时,质点的位置坐标是