题目内容
已知偶函数f(x)在[0,+∞)上是增函数,若f(x2-2x)<f(3),求实数x的取值范围.
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:根据函数奇偶性和单调性之间的关系,不等式等价为f(|x2-2x|)<f(3),利用单调性解不等式即可.
解答:
解:∵偶函数f(x)在[0,+∞)上是增函数,
∴不等式等价为f(|x2-2x|)<f(3),
即|x2-2x|<3,
即-3<x2-2x<3,
则
,
即
,
即
,
解得-1<x<3,
即不等式的解集为(-1,3).
∴不等式等价为f(|x2-2x|)<f(3),
即|x2-2x|<3,
即-3<x2-2x<3,
则
|
即
|
即
|
解得-1<x<3,
即不等式的解集为(-1,3).
点评:本题主要考查不等式的求解,根据函数奇偶性和单调性之间的关系,将不等式进行等转化是解决本题的关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
若关于x的不等式3x2+2ax+b≤0在区间[-1,0]上恒成立,则a2+b2-1的取值范围是( )
A、[
| ||
B、(-1,
| ||
C、[
| ||
D、(-1,
|
给定两个命题p,q,若¬p是q的必要而不充分条件,则p是¬q的( )
| A、必要而不充分条件 |
| B、充分而不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
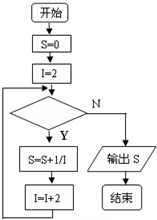
如图给出的是计算
+
+
+…+
的值的一个程序框图,其中判断框内应填入的条件是( )
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 100 |

| A、i≤100 | B、i>100 |
| C、i>50 | D、i≤50 |