题目内容
有以下四个命题：
①函数f（x）=sin（
-2x）的一个增区间是[
，
]；
②函数f（x）=sin（?x+φ）为奇函数的充要条件是φ为π的整数倍；
③对于函数f（x）=tan（2x+
），若f（x1）=f（x2），则x1-x2必是π的整数倍；
④函数f（x）=cos2x-sin2x，当x∈[
，π]时，f（x）的零点为（
，0）；
⑤y=cos|x+
|最小正周期为π；
其中正确的命题是 ．（填上正确命题的序号）
①函数f（x）=sin（
| π |
| 3 |
| 5π |
| 12 |
| 11π |
| 12 |
②函数f（x）=sin（?x+φ）为奇函数的充要条件是φ为π的整数倍；
③对于函数f（x）=tan（2x+
| π |
| 3 |
④函数f（x）=cos2x-sin2x，当x∈[
| π |
| 2 |
| 5π |
| 8 |
⑤y=cos|x+
| π |
| 3 |
其中正确的命题是
考点：命题的真假判断与应用
专题：三角函数的图像与性质
分析：①利用函数f（x）=sin（
-2x）的一个增区间，判断增区间是否是[
，
]，得到①正确；
②直接判断函数f（x）=sin（ωx+φ）为奇函数，则φ为π的整数倍，得到②正确；
③对于函数f（x）=tan（2x+
），利用f（x1）=f（x2），推出则x1-x2必是
的整数倍，得到③不正确；
④令f（x）=cos2x-sin2x=0，当x∈[
，π]时，得到f（x）的零点为x=
，得到④不正确；
⑤由y=cos|x+
|=cos（x+
）知，得到⑤不正确．
| π |
| 3 |
| 5π |
| 12 |
| 11π |
| 12 |
②直接判断函数f（x）=sin（ωx+φ）为奇函数，则φ为π的整数倍，得到②正确；
③对于函数f（x）=tan（2x+
| π |
| 3 |
| π |
| 2 |
④令f（x）=cos2x-sin2x=0，当x∈[
| π |
| 2 |
| 5π |
| 8 |
⑤由y=cos|x+
| π |
| 3 |
| π |
| 3 |
解答：
解：①因为函数f（x）=sin（
-2x）的单调增区间即求y=sin（2x-
）的递减区间，
由y=sin（2x-
）的递减区间2kπ+
≤2x-
≤2kπ+
（k∈Z），
解得[
+kπ，
+kπ]，k∈Z，
则它的一个增区间是[
，
]，所以①正确；
②若函数f（x）=sin（ωx+φ）为奇函数，则φ为π的整数倍，所以②正确；
③对于函数f（x）=tan（2x+
），若f（x1）=f（x2），则x1-x2必是
的整数倍，所以③错；
④f（x）=cos2x-sin2x=
cos（2x+
），令f（x）=0，得
cos（2x+
）=0，
又由x∈[
，π]时，则
≤2x+
≤
，∴2x+
=
，∴x=
，
即函数f（x）的零点是x=
，但不是点（
，0），所以④错；
对于⑤：由y=cos|x+
|=cos（x+
）知函数y=cos|x+
|周期为2π，所以⑤错．
故答案为：①②
| π |
| 3 |
| π |
| 3 |
由y=sin（2x-
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
解得[
| 5π |
| 12 |
| 11π |
| 12 |
则它的一个增区间是[
| 5π |
| 12 |
| 11π |
| 12 |
②若函数f（x）=sin（ωx+φ）为奇函数，则φ为π的整数倍，所以②正确；
③对于函数f（x）=tan（2x+
| π |
| 3 |
| π |
| 2 |
④f（x）=cos2x-sin2x=
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
又由x∈[
| π |
| 2 |
| 5π |
| 4 |
| π |
| 4 |
| 9π |
| 4 |
| π |
| 4 |
| 3π |
| 2 |
| 5π |
| 8 |
即函数f（x）的零点是x=
| 5π |
| 8 |
| 5π |
| 8 |
对于⑤：由y=cos|x+
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
故答案为：①②
点评：本题考查三角函数的有关性质，利用基本函数的基本性质解答问题，是解好数学问题的关键．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
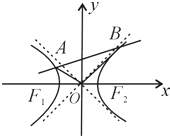如图，F1，F2是双曲线x2-y2=1的两个焦点，O为坐标原点，圆O是以F1F2为直径的圆，直线l：y=kx+b与圆O相切，并与双曲线交于A、B两点．
已知函数f（x）的定义域为[-1，5]，部分对应值如下表，