Question

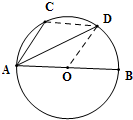
如图，AB是⊙O的直径，点C，D是半圆弧AB的两个三等分点，

AB

=

a

，

AC

=

b

，则

AD

=（　　）

• A、

  a

  -

  1

  2

  b

• B、

  1

  2

  a

  -

  b

• C、

  a

  +

  1

  2

  b

• D、

  1

  2

  a

  +

  b

Answer 1

考点：平面向量的基本定理及其意义

专题：计算题,平面向量及应用

分析：连结CD、OD，由圆的性质与等腰三角形的性质，证出CD∥AB且AC∥DO，得到四边形ACDO为平行四边形，所以

AD

=

AO

+

AC

，再根据题设条件即可得到用

a

、

b

表示向量

AD

的式子．

解答： 解：连结CD、OD，
∵点C、D是半圆弧AB的两个三等分点，
∴弧AC=弧BD，可得CD∥AB，∠CAD=∠DAB=

1

3

×90°=30°，
∵OA=OD
ADO=∠DAO=30°，
由此可得∠CAD=∠DAO=30°，
∴AC∥DO．
∴四边形ACDO为平行四边形，可得

AD

=

AO

+

AC

，
∵

AO

=

1

2

AB

=

1

2

a

，

AC

=

b

，
∴

AD

=

1

2

a

+

b

．
故选：D

点评：本题给出半圆弧的三等分点，求向量

AD

的线性表示式．着重考查了圆周角定理、平行四边形的判定与向量的线性运算等知识，属于中档题．