题目内容
在平面直角坐标系中,O是坐标原点,两定点A,B满足|
|=|
|=
•
=2,则点集{P|
=λ
+μ
,λ≥0,μ≥0,λ+μ≤1}所表示区域的面积为 .
| OA |
| OB |
| OA |
| OB |
| OP |
| OA |
| OB |
考点:简单线性规划,二元一次不等式(组)与平面区域,平面向量数量积的运算
专题:计算题,平面向量及应用
分析:由两定点A,B满足|
|=|
|=
•
=2,说明O,A,B三点构成边长为2的等边三角形,设出两个定点的坐标,再设出P点坐标,由平面向量基本定理,把P的坐标用A,B的坐标及λ,μ表示,把不等式0≤λ+μ≤1去绝对值后可得线性约束条件,画出可行域可求点集P所表示区域的面积.
| OA |
| OB |
| OA |
| OB |
解答:
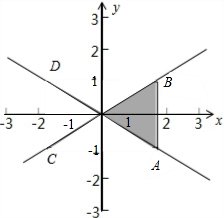 解:由两定点A,B满足|
解:由两定点A,B满足|
|=|
|=
•
=2,说明O,A,B三点构成边长为2的等边三角形.或∠AOB=120°的等腰三角形,
不妨O,A,B三点构成边长为2的等边三角形.
设A(
,-1),B(
,1).再设P(x,y).
由
=λ
+μ
,得:(x,y)=(
λ,-λ)+(
μ,μ)=(
(λ+μ),μ-λ).
所以
,解得
①.
由λ+μ≤1.
所以①等价于
可行域如图中矩形ABCD及其内部区域,
则区域面积为
.
故答案为:
.
 解:由两定点A,B满足|
解:由两定点A,B满足|| OA |
| OB |
| OA |
| OB |
不妨O,A,B三点构成边长为2的等边三角形.
设A(
| 3 |
| 3 |
由
| OP |
| OA |
| OB |
| 3 |
| 3 |
| 3 |
所以
|
|
由λ+μ≤1.
所以①等价于
|
则区域面积为
| 3 |
故答案为:
| 3 |
点评:本题考查了平面向量的基本定理及其意义,考查了二元一次不等式(组)所表示的平面区域,考查了数学转化思想方法,解答此题的关键在于读懂题意,属中档题.

练习册系列答案
相关题目
 一个几何体的三视图及部分数据如图所示,正视图、侧视图和俯视图都是等腰直角三角形,则该几何体的体积为( )
一个几何体的三视图及部分数据如图所示,正视图、侧视图和俯视图都是等腰直角三角形,则该几何体的体积为( )A、
| ||
B、
| ||
C、
| ||
| D、1 |
已知关于x的不等式ax2-ax-2a2>1(a>0且a≠1)的解集为{x|-a<x<2a};且函数f(x)=
的定义域为R,则m的范围为( )
(
|
| A、[-1,0] | B、(0,1) |
| C、(1,+∞) | D、φ |
 某几何体的三视图如所示,该几何体的体积为( )
某几何体的三视图如所示,该几何体的体积为( )| A、20 | ||
B、
| ||
| C、56 | ||
| D、60 |
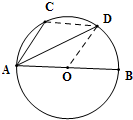
如图,AB是⊙O的直径,点C,D是半圆弧AB的两个三等分点,
=
,
=
,则
=( )
| AB |
| a |
| AC |
| b |
| AD |

A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 一个正三棱柱的三视图如图所示,则a=
一个正三棱柱的三视图如图所示,则a=