题目内容
若sin(π-a)=-
,且a∈(π,
),则sin(
+
)=( )
| ||
| 3 |
| 3π |
| 2 |
| π |
| 2 |
| a |
| 2 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
考点:诱导公式的作用,同角三角函数间的基本关系
专题:三角函数的求值
分析:已知等式利用诱导公式化简求出sinα的值,根据α的范围,利用同角三角函数间的基本关系求出cosα的值,再利用二倍角的余弦函数公式求出cos
的值,所求式子利用诱导公式化简,将cos
的值代入计算即可求出值.
| α |
| 2 |
| α |
| 2 |
解答:
解:∵sin(π-α)=sinα=-
,且α∈(π,
),
∴cosα=-
=-
=-
,
∵cosα=2cos2
-1,
∈(
,
),
∴cos
=-
=-
=-
,
则sin(
+
)=cos
=-
.
故选B
| ||
| 3 |
| 3π |
| 2 |
∴cosα=-
| 1-sin2α |
1-(-
|
| 2 |
| 3 |
∵cosα=2cos2
| α |
| 2 |
| α |
| 2 |
| π |
| 2 |
| 3π |
| 4 |
∴cos
| α |
| 2 |
|
|
| ||
| 6 |
则sin(
| π |
| 2 |
| α |
| 2 |
| α |
| 2 |
| ||
| 6 |
故选B
点评:此题考查了诱导公式的作用,以及同角三角函数间的基本关系,熟练掌握公式是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设A(3,2,1),B(1,0,5),C(0,2,1),AB的中点为M,则|CM|=( )
| A、3 | ||
B、
| ||
C、2
| ||
D、3
|
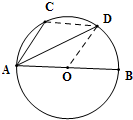
如图,AB是⊙O的直径,点C,D是半圆弧AB的两个三等分点,
=
,
=
,则
=( )
| AB |
| a |
| AC |
| b |
| AD |

A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 一个正三棱柱的三视图如图所示,则a=
一个正三棱柱的三视图如图所示,则a=